Solve problem in this form\[ [13,4,15],[9,3,20], \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}\]

Given vector A = [2, -1, 3] and vector B = [4, 2, -2], enter the expression this way
[ 2, -1, 3 ] , [ 4, 2, -2 ]
A vector cross product, also known as a vector product, is an operation that takes two vectors and generates a third vector that is perpendicular to both of the original vectors. It is denoted by the symbol "x" or using the cross product notation.
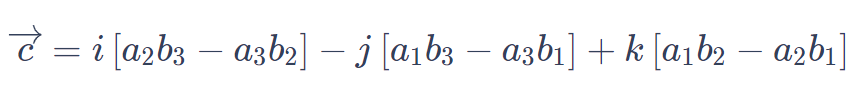
To solve a vector cross product, follow these steps:
1. Identify the two vectors that you want to find the cross product of. Let's call them vector A and vector B.
2. Write down the components of each vector. For example, vector A can be represented as [A₁, A₂, A₃] and vector B can be represented as [B₁, B₂, B₃].
3. Calculate the cross product by following the steps:
The x-component of the cross product is calculated as: (A₂ B₃) - (A₃ B₂)
The y-component of the cross product is calculated as: (A₃ B₁) - (A₁ B₃)
The z-component of the cross product is calculated as: (A₁ B₂) - (A₂ B₁)
4. Combine the components to obtain the resulting vector. The cross product vector will be in the form [x, y, z].
Given vector A = [2, -1, 3] and vector B = [4, 2, -2], the task is to find the cross product of these vectors.
we have:
The x-component of the cross product = (2 * 2) - (-1 * -2) = 4 - 2 = 2
The y-component of the cross product = (3 * 4) - (2 * 2) = 12 - 4 = 8
The z-component of the cross product = (2 * -2) - (4 * -1) = -4 - (-4) = -4 + 4 = 0
Therefore, the cross product of vector A and vector B is [2, 8, 0].
