Solve combination in this form \[^nC_r=\frac{n!}{r!\left(n-r\right)!} \]
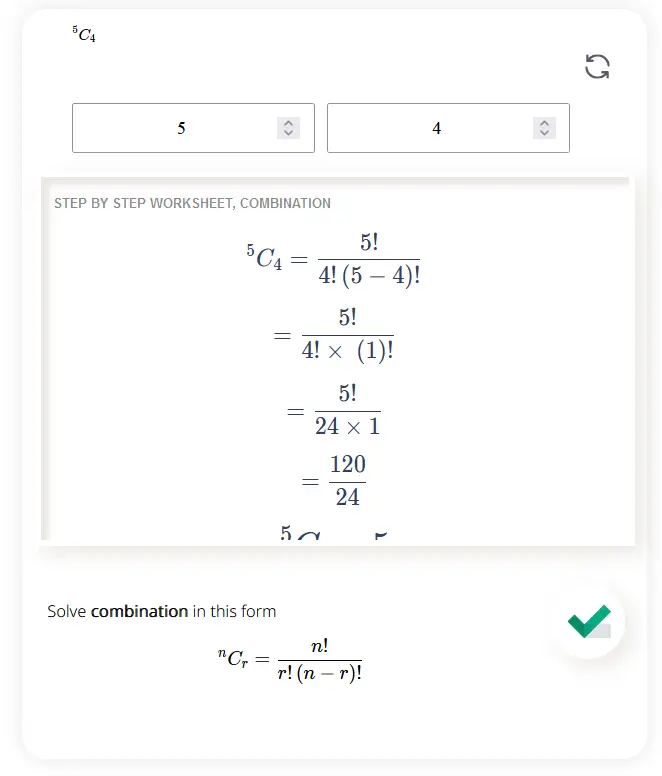
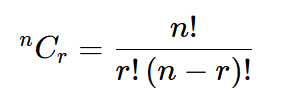
A combination is the number of selections of different items from distinguishable items when order of selection is ignored.
In algebra, combinations refer to the selection of a group of objects from a larger set, where the order of the objects does not matter. The number of combinations can be found using the formula:
where n represents the total number of objects and r represents the number of objects being selected.
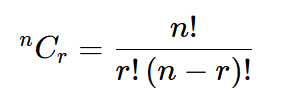
1. Probability: Combinations are used to calculate the number of favorable outcomes in an event. For example, determining the number of possible outcomes in a game of poker or in rolling dice.
2. Genetics: Combinations are used in genetics to calculate the possible combinations of genes and alleles in the offspring.
3. Combinatorial optimization: Combinations are used to solve optimization problems, such as finding the most efficient route for delivery trucks to visit multiple locations.
4. Combinatorics: Combinations are a fundamental concept in combinatorics, which studies the arrangement and selection of objects.
5. Data analysis: Combinations are used in data analysis to calculate the number of possible subsets or combinations of variables, which can provide insights into patterns and relationships in the data.
6. Cryptography: Combinations are used in cryptography to generate secure passwords or encryption keys by randomly selecting combinations of characters or numbers.
7. Computer science: Combinations are used in algorithms and data structures, such as generating permutations or subsets of a set.
8. Game theory: Combinations are used in game theory to analyze the possible combinations of strategies and outcomes in games.
C(8, 4) = 8! / (4!(8 - 4)!)
= 8! / (4! 4!)
We can simplify this expression as:
8! = 8 x 7 x 6 x 5 x 4! = 8 7 6 5 4
4! = 4 x 3 x 2 x 1
Substituting these values back into the formula:
C(8, 4) = (8 x 7 x 6 x 5 x 4) / (4 x 3 x 2 x 1)
This can be further simplified as:
C(8, 4) = (8 x 7 x 6 x 5) / (4 x 3 x 2 x 1)
