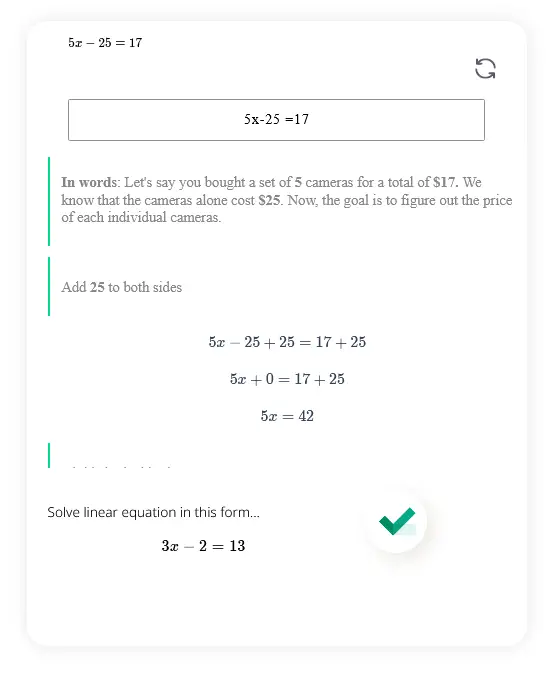
Solve linear equation in this form... \[3x - 2 =13 \]
A linear equation is an equation that represents a straight line when graphed on a coordinate plane. It is an equation of the form y = mx + b, where x and y are variables, m is the slope of the line, and b is the y-intercept (the point where the line crosses the y-axis). Linear equations can also be written in standard form as Ax + By = C, where A, B, and C are constants. Linear equations are commonly used in mathematics and real-life situations to model relationships and make predictions.
An algebraic expression is a combination of variables, constants, and mathematical operations, without an equal sign. It represents a mathematical statement or relationship that can be simplified, evaluated, or manipulated algebraically. Examples of algebraic expressions include:
1. 3x + 2y
2. 4a - 5b + 7
3. 2(x + y) - 3z
An algebraic equation, on the other hand, is a statement that asserts the equality of two algebraic expressions. It has an equal sign, and the goal is to find the values of the variables that make the equation true. Examples of algebraic equations include:
1. 2x + 1 = 7
2. 3(a + 2) = 15
3. 4x - 5y = 10
Let's solve the equation: 2(3x + 5) - 4 = 8
Step 1: Distribute the 2 to the terms inside the brackets: 6x + 10 - 4 = 8
Step 2: Combine like terms: 6x + 6 = 8
Step 3: Subtract 6 from both sides to isolate the variable: 6x = 2
Step 4: Divide both sides by 6 to solve for x: x = 2/6
Step 5: Simplify the fraction: x = 1/3
Step 6: Double-check the solution by substituting it back into the original equation: 2(3(1/3) + 5) - 4 = 8
Simplifying further: 2(1 + 5) - 4 = 8
Calculating: 2(6) - 4 = 8
Calculating: 12 - 4 = 8
Calculating: 8 = 8
Since the left side of the equation (8) is equal to the right side of the equation (8), we have validated the solution.
Solve the equation: 3/4x + 1/2 = 5/6
Step 1: To get rid of the fractions, we can multiply each term in the equation by the least common multiple (LCM) of the denominators. In this case, the LCM of 4, 2, and 6 is 12.
(12) (3/4x) + (12) (1/2) = (12) * (5/6)
Step 2: Simplify the equation by multiplying.
9x + 6 = 10
Step 3: Next, we want to isolate the variable 'x'. Subtract 6 from both sides of the equation.
9x + 6 - 6 = 10 - 6
9x = 4
Step 4: Solve for 'x' by dividing both sides of the equation by 9.
9x/9 = 4/9
x = 4/9
Step 5: The solution is x = 4/9.
Step 6: Double-checking the solution, we can substitute x = 4/9 back into the original equation and see if it holds true.
(3/4 * 4/9) + 1/2 = 5/6
(12/36) + 1/2 = 5/6
1/3 + 1/2 = 5/6
2/6 + 3/6 = 5/6
5/6 = 5/6
The equation holds true, confirming that the solution x = 4/9 is correct.
So, the linear equation 3/4x + 1/2 = 5/6 is solved and the solution is x = 4/9.
