Angle Between Two Vectors in a 2D solver

About The Calculator

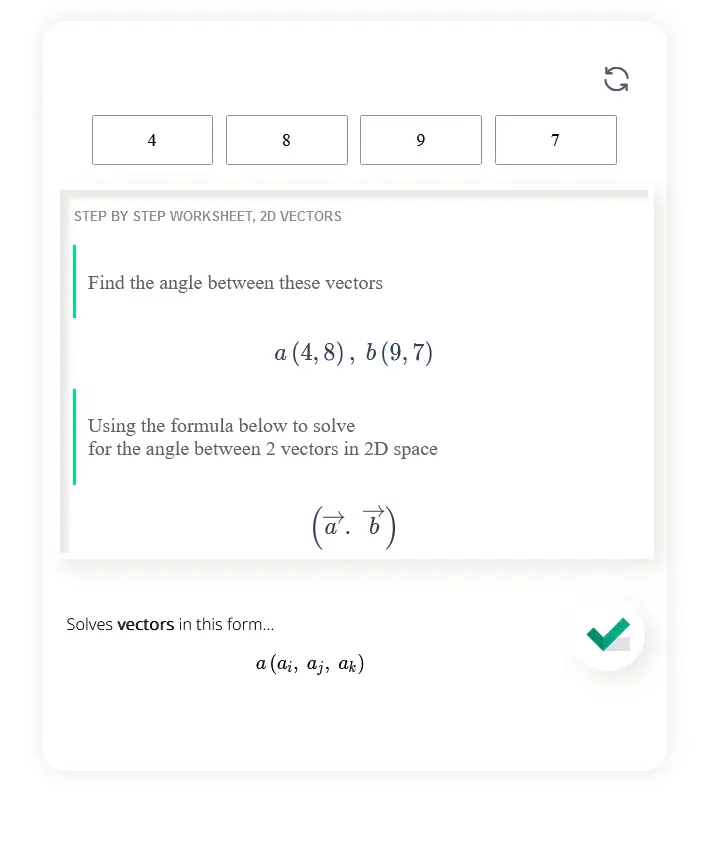
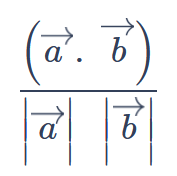
Angle between two vectors calculator computes the angle between two vectors in a 2D space. A 2D Vector is a vector geometry in 2-dimensions running from point A (tail) to point B (head). Each vector has a magnitude (or length) and direction and can be calculated by taking the square root of the sum of each components in space.

Lesson Note on Angle Between Two Vectors

To illustrate the calculation of the angle between two vectors in a 2D space, let's consider the following example:

Example 1

Let's say we have two vectors in a 2D space:

• Vector A with magnitude 3 and direction 45 degrees counterclockwise from the positive x-axis.

• Vector B with magnitude 2 and direction 30 degrees counterclockwise from the positive x-axis.

Step 1: Represent the vectors graphically

Draw a coordinate system with the x-axis and y-axis. Place the tail of Vector A at the origin (0,0) and draw the arrow pointing towards point B. Similarly, place the tail of Vector B at the origin and draw the arrow pointing towards point C.

Step 2: Calculate the components of each vector

To calculate the components of Vector A, we need to determine its x-component (Ax) and y-component (Ay). Since Vector A is 45 degrees counterclockwise from the positive x-axis, we can use trigonometry to find these components:

Ax = magnitude of A cos(angle of A)
= 3 cos(45 degrees)
= 3 * sqrt(2) / 2
= 3sqrt(2) / 2

Ay = magnitude of A sin(angle of A)
= 3 sin(45 degrees)
= 3 * sqrt(2) / 2
= 3sqrt(2) / 2

Similarly, we can calculate the components of Vector B:

Bx = magnitude of B cos(angle of B)
= 2 cos(30 degrees)
= 2 * sqrt(3) / 2
= sqrt(3)

By = magnitude of B sin(angle of B)
= 2 sin(30 degrees)
= 2 * 1/2
= 1

Step 3: Calculate the dot product of the vectors

The dot product of two vectors is calculated by multiplying their corresponding components and summing them up:
Dot product (A · B) = Ax Bx + Ay By

= (3sqrt(2) / 2) sqrt(3) + (3sqrt(2) / 2) 1
= 3sqrt(6) / 2 + 3sqrt(2) / 2
= (3sqrt(6) + 3sqrt(2)) / 2

Step 4: Calculate the magnitudes of the vectors

The magnitude of a vector is the length or size of the vector and can be calculated using the Pythagorean theorem:
Magnitude of A = sqrt(Ax^2 + Ay^2)
= sqrt((3sqrt(2) / 2)^2 + (3sqrt(2) / 2)^2)
= sqrt(9/2 + 9/2)
= sqrt(9)
= 3

Magnitude of B = sqrt(Bx^2 + By^2)
= sqrt((sqrt(3))^2 + 1^2)
= sqrt(3 + 1)
= sqrt(4)
= 2

Step 5: Calculate the angle between the two vectors

The angle between two vectors can be found using the dot product and the magnitudes of the vectors:

Angle between A and B (θ) = cos^(-1)((A · B) / (magnitude of A * magnitude of B))

= cos^(-1)(((3sqrt(6) + 3sqrt(2)) / 2) / (3 * 2))
= cos^(-1)((3sqrt(6) + 3sqrt(2)) / 6)
= cos^(-1)(sqrt(6) + sqrt(2)) / 2

Therefore, the angle between Vector A and Vector B in this example is cos^(-1)((sqrt(6) + sqrt(2)) / 2).

Example 2: find the angle between two vectors in 2D space, you can use the dot product formula. The formula is as follows:

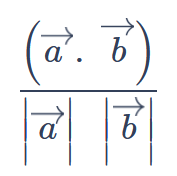
θ = arccos( (a · b) / (|a| * |b|) )

Step 1: Find the dot product of vectors a and b.

a · b = (3 2) + (4 8)

= 6 + 32

= 38

Step 2: Find the magnitude (length) of vector a.

|a| = √(3^2 + 4^2)

= √(9 + 16)

= √25

= 5

Step 3: Find the magnitude (length) of vector b.

|b| = √(2^2 + 8^2)

= √(4 + 64)

= √68

≈ 8.246

Step 4: Substitute the values in the formula to find the angle.

θ = arccos( 38 / (5 * 8.246) )

Step 5: Use a calculator to find the arccos of the number.

θ ≈ arccos(0.91892)

≈ 23.57 degrees (rounded to two decimal places)

Therefore, the angle between vectors a(3, 4) and b(2, 8) in 2D space is approximately 23.57 degrees.