Solves problem in this form \[\frac{x_1}{y_1}=\frac{x_2}{k}\]
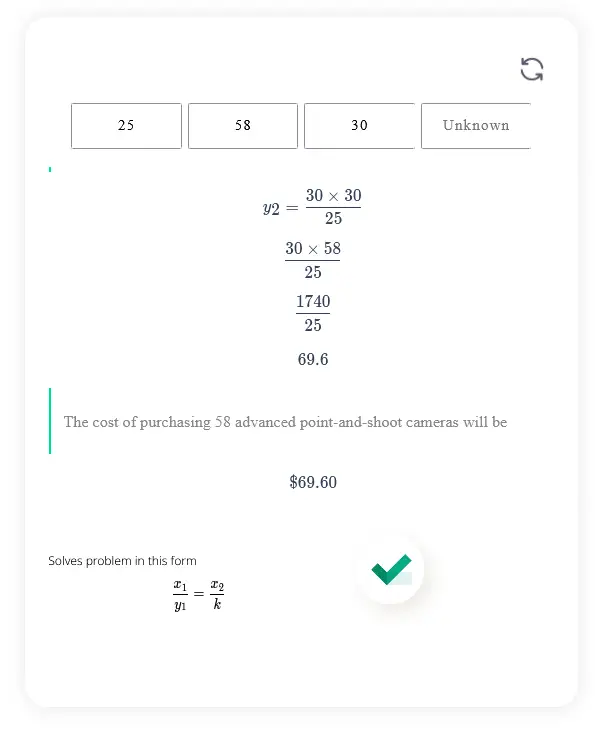
Direct proportion refers to a situation in which two values increase or decrease together in the same way. If one value increases by a certain amount, the other value also increases by the same amount. If one decreases, then the other also decreases. In a direct proportion, the ratio of two values is always the same. The direct proportion calculator even makes it easier than ever to compute for the unknown in a record time.
1. Identify the two variables involved in the proportion. These will be referred to as x and y.
2. Write down the proportion. The written proportion should be in the form “x is directly proportional to y”.
3. Find a pair of values that illustrates the proportion. For example, if x = 2 and y = 4, this is an example of a direct proportion since x is directly proportional to y.
4. Use the given pair of values to calculate the ratio. In the example, the ratio is 2:4, which can also be written as 1:2.
5. Use the ratio to calculate the value of the unknown variable. For example, if x = 6, then you can use the ratio to calculate that y = 12 (since 6 is twice as much as 3 and 12 is twice as much as 6).
6. Use the direct proportion calculator to check your answer. In the example, if x = 6 and y = 12, then 6 is double 3 and 12 is double 6, which satisfies the condition that x is directly proportional to y.ratios and proportions. It can also help us understand how changes in one variable can affect another variable and vice versa.
