Solves vectors in this form \[a\left(a_i,\ a_j,\ a_k\right), \ b\left(b_i,\ b_j,\ b_k\right)\]
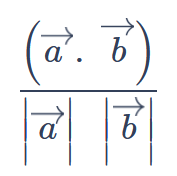
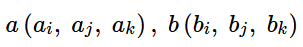
Angle between two vectors calculator computes the angle between two vectors in a 3D space. A 3D Vector is a vector geometry in 2-dimensions running from point A (tail) to point B (head). Each vector has a magnitude (or length) and direction and can be calculated by taking the square root of the sum of each components in space.
Vectors are quantities defined by magnitude and direction. The geometrical representation of a vector is by means of an arrow whose length, to some scale, represents the magnitude of the physical quantity and whose direction indicates the direction of the vector.
A scalar quantity is one which is completely defined by its magnitude. To distinguish the magnitude of a vector a from its direction we use the mathematical notation
If the components of a vector in a rectangular coordinate system are known. To distinguish the magnitude of a vector a from its direction we use the mathematical notation. Since the vector and its components form a right-angled triangle, we have the magnitude of a vector defined as where r = magnitude or modulus of Z and is written as mod Z or |z|. Note the actual value of r is determined by using Pythagoras' theorem
The θ is called the argument (or amplitude) of Z and is written as arg Z. By trigonometry on triangle, argument or amplitude of Z is derived from the division of imaginary path by real path on y and x axis respectively
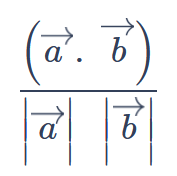
To find the angle between two vectors in 3D space, we can use the dot product formula:
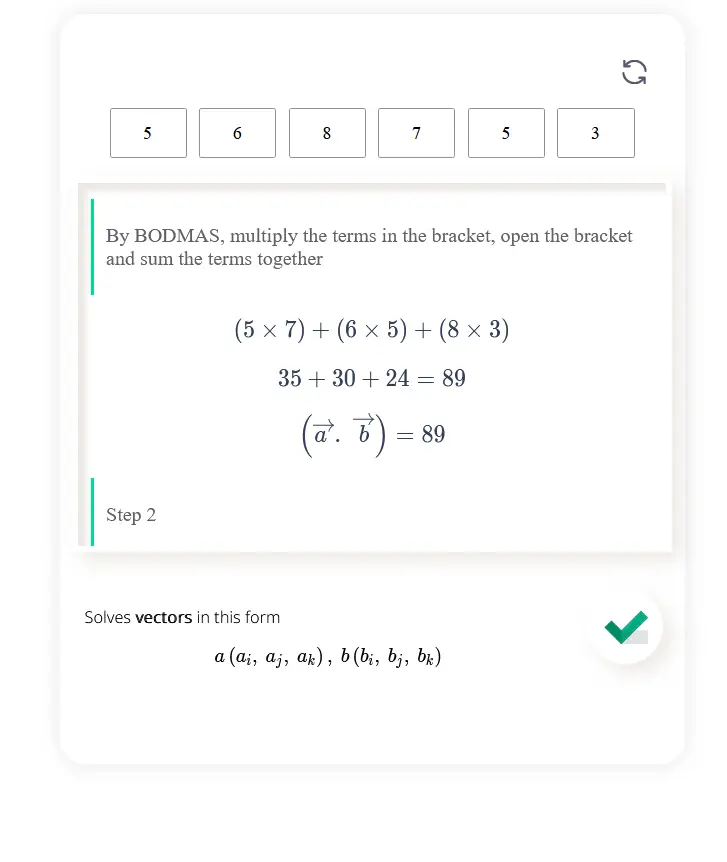
θ = cos⁻¹((𝑎•𝑏) / (||𝑎|| ||𝑏||))
where 𝑎 and 𝑏 are the two vectors and • represents the dot product operation. ||𝑎|| and ||𝑏|| represent the magnitudes of the vectors.
1. Identify the two vectors 𝑎 and 𝑏 in the problem.
2. Calculate the dot product (𝑎•𝑏) and the magnitudes ||𝑎|| and ||𝑏||.
3. Substitute these values into the formula θ = cos⁻¹((𝑎•𝑏) / (||𝑎|| ||𝑏||)) and solve for θ.
4. Check your answer by substituting it back into the original problem or using alternative methods to verify its accuracy.
5. If necessary, convert the angle from radians to degrees or vice versa, depending on the problem's requirements.
