Solves \[\frac{\log A -\log B+\frac{c}{d}\log E}{F \log G}\]
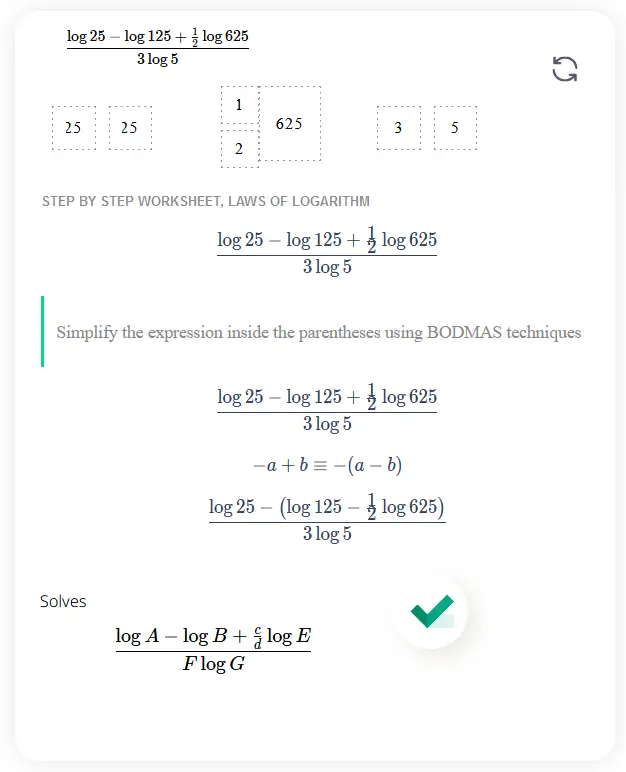
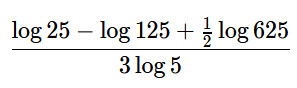
Logarithms rules are mathematical rules that govern the manipulation and simplification of logarithmic expressions and equations. These rules help in solving logarithmic equations and simplifying expressions involving logarithms.
To simplify the logarithmic equation
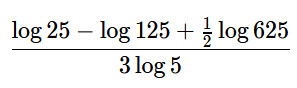
Apply logarithmic rules and properties.
First, let's simplify the logarithmic terms:
log(25) = log(5^2) = 2 log(5)
log(125) = log(5^3) = 3 log(5)
log(625) = log(5^4) = 4 log(5)
Using these simplified terms, we can rewrite the logarithmic equation as:
(2 log(5) - 3 log(5) + 1/2 * 4 log(5)) / 3 log(5)
Next, let's simplify the numerator:
(2 log(5) - 3 log(5) + 2 log(5)) / 3 log(5)
(log(5)) / 3 log(5)
Therefore, the simplified form of the logarithmic equation
(log(25) - log(125) + 1/2*log(625)) / 3 log(5) is 1/3.
1. What is the purpose of logarithmic rules?
Logarithmic rules are used to simplify and manipulate logarithmic expressions and equations. They help in solving logarithmic equations and simplifying complex logarithmic terms.
2. How do logarithmic rules help in solving equations?
Logarithmic rules allow us to rewrite complex equations involving exponents as simpler equations involving logarithms. This makes it easier to solve for the unknown variable.
3. Can logarithmic rules be used with different bases?
Yes, logarithmic rules can be applied to logarithms with different bases. The change of base formula allows us to convert between different bases and apply the logarithmic rules accordingly.
4. Are there any restrictions or limitations when applying logarithmic rules?
It is important to use logarithmic rules carefully and consider any restrictions or limitations. For example, logarithms are only defined for positive values, so the argument of the logarithm must be positive. Division by zero is also not allowed.
5. How do logarithmic rules relate to exponential functions?
Logarithmic rules are closely related to exponential functions. They provide a way to manipulate exponential equations and simplify them using logarithmic expressions.
