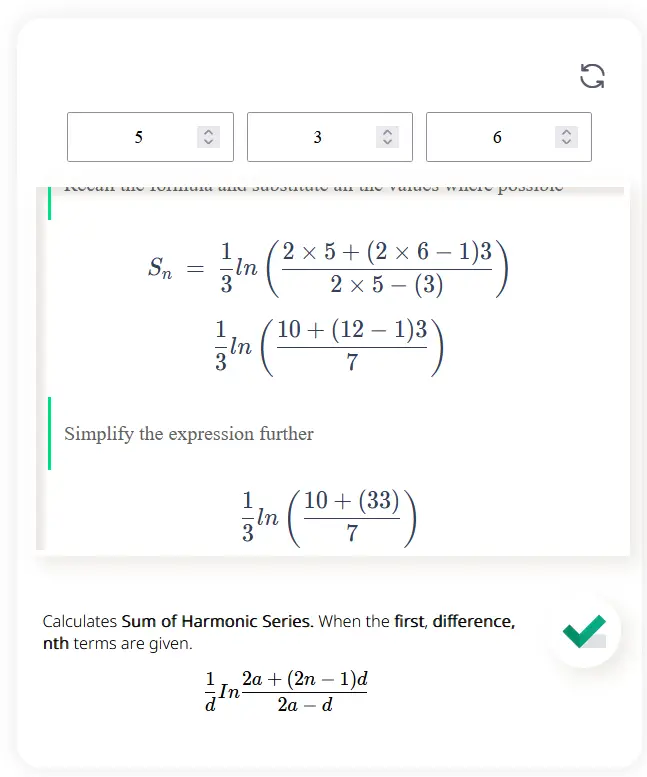
Calculates Sum of Harmonic Series. When the first, difference, nth terms are given.\[\frac{1}{d} In \frac{2a+(2n-1)d}{2a-d}\]
Harmonic progression series is a sequence of numbers in which the reciprocal of each term forms an arithmetic progression. In other words, it is a series where the difference between consecutive terms is a constant ratio.
The general form of a harmonic progression series is 1/a, 1/(a+d), 1/(a+2d), ..., where a is the first term and d is the common difference.
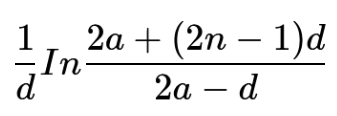
1. Understand the concept of a harmonic series: A harmonic series is an infinite series of the form 1 + 1/2 + 1/3 + 1/4 + ... + 1/n. It is called a harmonic series because each term is the reciprocal of a positive integer.
2. Determine the type of harmonic series: There are different types of harmonic series, such as the regular harmonic series (1 + 1/2 + 1/3 + ...) or alternate harmonic series (1 - 1/2 + 1/3 - ...). Identify which type you are working with.
3. Define the series as an infinite sequence: Write down the series as a sum of terms using sigma notation or simply as a sequence.
4. Check for convergence or divergence: Determine whether the series converges (the sum approaches a finite value) or diverges (the sum goes to infinity) by applying convergence tests or evaluating limits.
5. Apply the appropriate convergence test: Some common convergence tests for a harmonic series include the divergence test, comparison test, integral test, and limit comparison test.
6. Evaluate the limit or perform the comparison: In most cases, you will need to evaluate the limit of the terms or compare the series to another known convergent or divergent series.
7. State the result: If the series converges, state the sum as a finite value. If it diverges, indicate that the series does not have a finite sum and explain why.
8. Check for conditional convergence (only for alternate harmonic series): If you are dealing with an alternate harmonic series, check if it converges conditionally by examining the partial sums of the positive and negative terms separately.
9. Apply any additional tests or methods (optional): Depending on the specific problem or situation, you may need to apply additional tests or methods to determine convergence or divergence.
10. Provide a clear and concise solution: Summarize the steps and provide a final solution or conclusion to the problem, indicating whether the harmonic series converges or diverges and, if applicable, the sum of the series.
