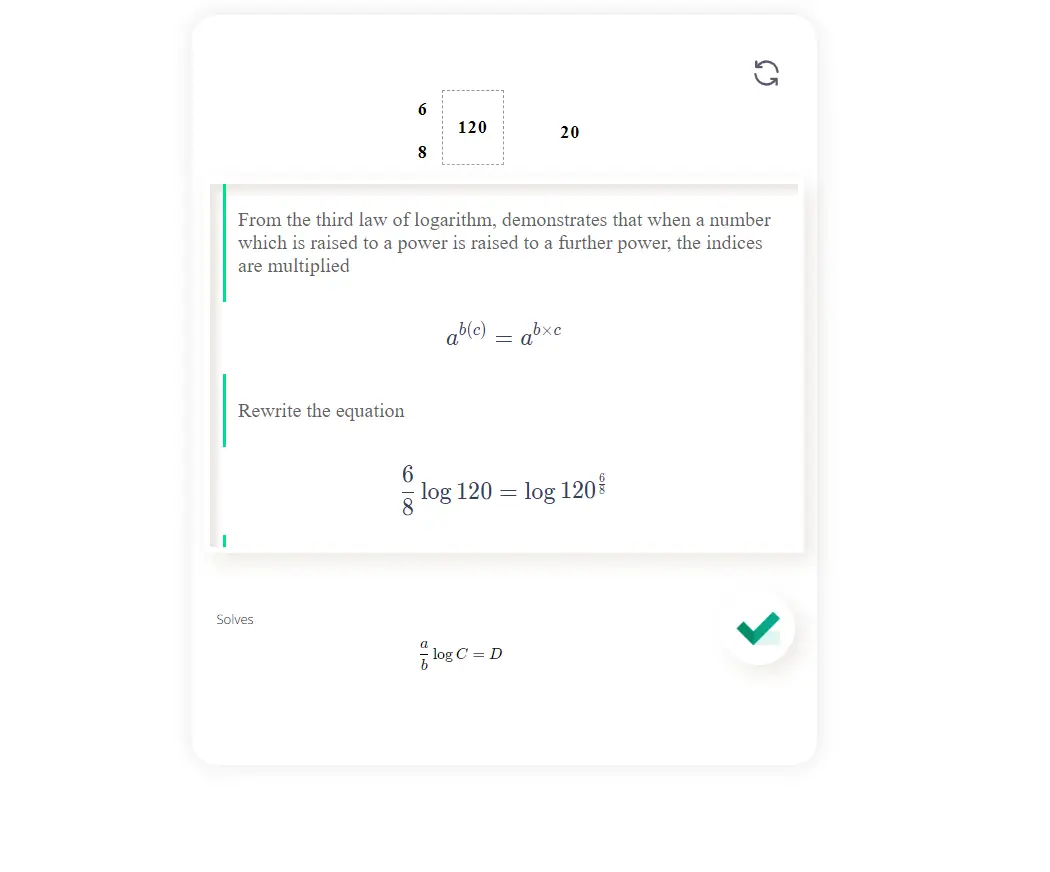
Solves \[\frac{a}{b}\log C=D\]
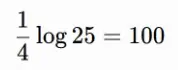
Logarithms are mathematical functions that represent the inverse of exponential functions. They are used to solve equations involving exponential growth or decay, and to simplify complex calculations.
The power rule of logarithms states that for any positive numbers b, k, and x, and any positive base other than 1, the following properties hold:
Logarithm of a power: log base b (x^k) = k * log base b (x)
The relationship between power, index, and base can be illustrated through the concept of exponentiation and root operations.
Exponentiation is a mathematical operation that involves raising a base to a certain power. The power represents the exponent to which the base is raised.
For example, in the expression 2^3, the base is 2 and the power is 3.
This means that 2 is multiplied by itself three times: 2 * 2* 2 = 8.
Root operations, on the other hand, involve finding the number that, when raised to a certain power (index), equals a given value.
For example, the square root is a type of root operation with an index of 2. It finds the number that, when squared, equals a given value.
In the expression √9, the index is 2 and the value is 9.
The square root of 9 is 3 because 3^2 = 9.
To illustrate the relationship between power, index, and base, consider the expression
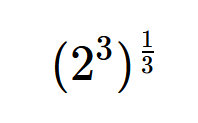
In this expression, we raise 2 to the power of 3 and then take the cube root of the result.
First, we calculate 2^3:
2^3 = 2 *2 * 2 = 8.
Next, we take the cube root of 8:
∛8 = 2.
Therefore, (2^3)^(1/3) = 2, showing the relationship between power, index, and base.
Simplify log base 2 (8) using the power rule.
log base 2 (8) = log base 2 (2^3)
Applying the power rule, we have:
log base 2 (8) = 3 * log base 2 (2)
Since log base 2 (2) equals 1, the equation simplifies to:
Simplify log base 5 (125)
log base 5 (125) = log base 5 (5^3)
Applying the power rule, we have:
log base 5 (125) = 3 * log base 5 (5)
Since log base 5 (5) equals 1, the equation simplifies to:
Simplify log base 3 (27^2) using the power rule.
log base 3 (27^2) = 2 * log base 3 (27)
Since 27 is equal to 3^3, the equation becomes:
log base 3 (27^2) = 2 * log base 3 (3^3)
Using the power rule again, we have:
log base 3 (27^2) = 2 * 3
Simplifying further, we get:
Simplify log base 4 (16/2) using the power rule.
log base 4 (16/2)
= log base 4 (16) - log base 4 (2)
Applying the power rule, we have:
log base 4 (16/2) = log base 4 (4^2) - log base 4 (2)
Since 4 is equal to 2^2, the equation simplifies to:
log base 4 (16/2) = log base 4 (2^2^2) - log base 4 (2)
Using the power rule again, we have:
log base 4 (16/2) = 2 * log base 4 (2) - log base 4 (2)
Since log base 4 (2) equals 1, the equation simplifies to:
log base 4 (16/2) = 2 - 1
Simplifying further, we get:
