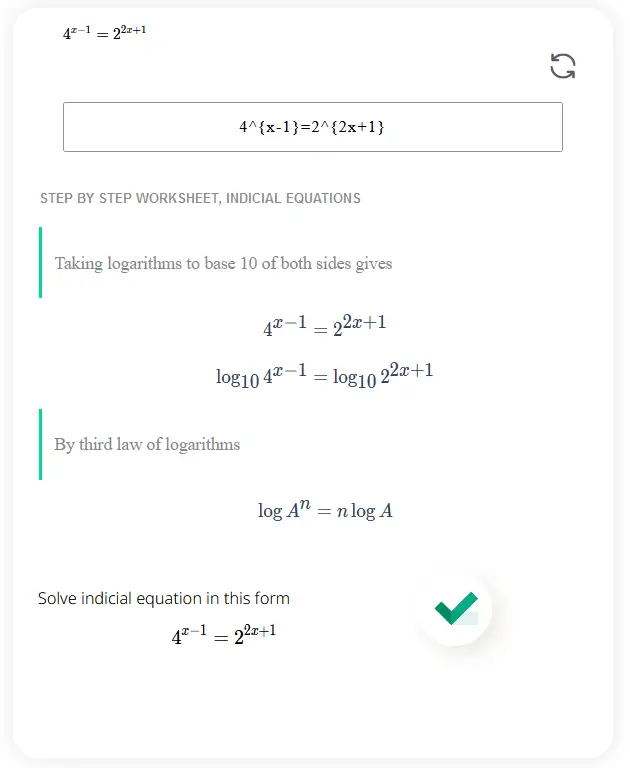
Solve indicial equation in this form \[4^{x-1} = 2^{2x+1}\]
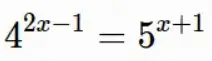
Solving equations involving powers, also known as indicial equations, can be simplified using logarithms. By taking the logarithm of both sides of an equation like 3^x = 81, with a base of 10, you can easily find the value of x.
MathCrave indicial equation solver or calculator help convert exponential equations into manageable forms. This calculator use logarithmic properties, rewrite the equation and solve complex expression in the following format
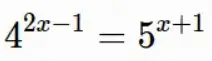
4^{2x+1}=5^{2x+2}
2^{x+1}=3^{x+5}
5^{2x-1}=5^{x-7}
2^{x+1}=3^{2x-5}
Start by taking the logarithm of both sides of the equation. Since the given equation has different bases, you can use the logarithmic identity
log_b(a^c) = c * log_b(a).
Applying this identity, we get:
log_4(4^{x-1}) = log_4(2^{2x+1})
Simplify the logarithms using the power rule of logarithms. The power rule states that log_b(a^c) = c * log_b(a).
Applying this rule, we have:
(x-1) log_4(4) = (2x+1) log_4(2)
Simplifying further:
(x-1) = (2x+1) log_4(2)
Expand the logarithm base to base 10. Using the change of base formula, we can rewrite the equation as:
(x-1) = (2x+1) log_2(4)/log_2(10)
Since log_2(4) = 2 and log_2(10) is a constant value, we can substitute these values into the equation:
(x-1) = (2x+1) (2/ log_2(10))
Solve for x. Distribute the (2/ log_2(10)) term:
(x-1) = (4/ log_2(10))x + (2/ log_2(10))
Rearrange the equation to solve for x
(x - (4/ log_2(10))x) = 1 + (2/ log_2(10))
Simplify
(x(1 - 4/ log_2(10))) = (1 + 2/ log_2(10))
Combine like terms
x(1 - 4/ log_2(10)) = (log_2(10) + 2)/ log_2(10)
x = (log_2(10) + 2)/ (log_2(10) - 4/ log_2(10))
Using a calculator, we can evaluate log(2):
log(2) ≈ 0.3
Substitute this value below to resolve for x
(x-1) = (4/ log_2(10))x + (2/ log_2(10))
