Solve elevation using this formula \[\angle=\frac{h}{s} \]
Angle of elevation solver calculates angle through which the imaginary straight line must be raised (or elevated) from the horizontal level of any given object. If the imaginary line were to be lowered (depressed) from the ground, it becomes angle of depression.
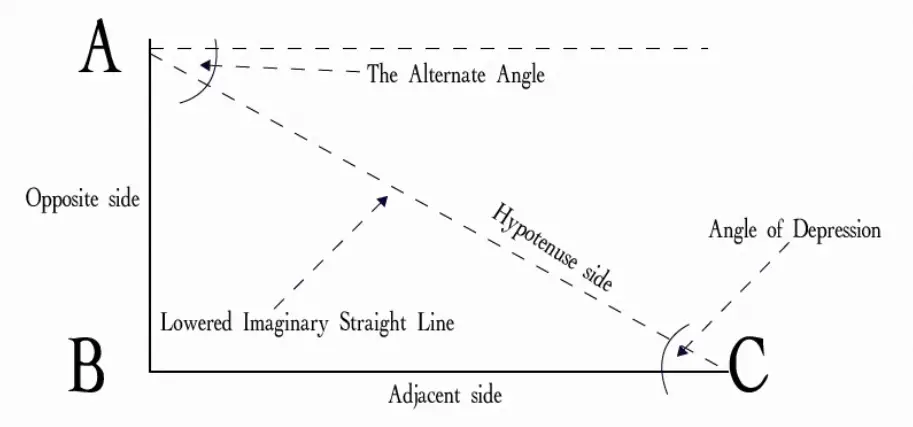
The angle of elevation is the angle between the horizontal line of sight and the line of sight from an observer to a higher point or object. It is typically measured in degrees.
Enter the value for distance and height into the box (numbers only)
Hit the check mark button to generate the worksheet.
Suppose you want to find out the height of a tall tree in your backyard, but you cannot directly measure it. You can use the angle of elevation to solve this problem. Stand at a specific distance from the tree and measure the angle between your eye level and the top of the tree. Then, knowing the distance between you and the tree, you can use trigonometry (specifically, the tangent function) to calculate the height of the tree. By applying the angle of elevation, you can determine the height of the tree without actually climbing it
Imagine you are standing some distance away from a skyscraper and want to know its height. By measuring the angle of elevation from your eye level to the top of the building, you can use trigonometry to calculate its height. Similar to the tree example, you need to measure the angle and the distance between you and the building. By applying the tangent function, you can determine the height of the building. Angle of elevation can help you estimate the height of tall structures without physically measuring it
When setting up security cameras, it is important to position them correctly for optimal surveillance. The angle of elevation plays a crucial role in determining the camera's field of view. By calculating the appropriate angle of elevation, you can ensure that the camera captures the desired area without any obstructions. By understanding the concept of the angle of elevation, you can strategically position security cameras for effective surveillance in real-life scenarios.
A person standing at point A looks up at the top of a building. The angle of elevation from the person's eye to the top of the building is 30 degrees. The person then moves 50 meters closer to the building and looks up again. This time, the angle of elevation from the person's eye to the top of the building is 45 degrees. How tall is the building?
Let's assume that the height of the building is represented by h meters. We can set up a right triangle to represent the situation. The vertical side of the triangle represents the height of the building, the horizontal side represents the distance between the person and the building, and the hypotenuse represents the line of sight from the person's eye to the top of the building
Step 1
First, let's consider the triangle when the person is at point A. In this case, the angle of elevation is30 degrees. We can use the tangent function to relate the angle and the sides of the triangle: tan(30) = h / x, where x is the distance between the person and the building
Step 2
Let's consider the triangle when the person moves 50 meters closer to the building. In this case, the angle of elevation is 45 degrees. We can again use the tangent function:tan(45) = h / (x -50)
Now, we have a system of two equations with two unknowns (h and x). You can solve this system by substituting one equation into the other: (h / x) = tan(30)(h / (x -50)) = tan(45)
By substituting h / x in the second equation with
tan(30), we get:(tan(30) / (x -50)) = tan(45)
Now, you can solve for x:tan(30) / (x -50) = tan(45)(x -50) = tan(30) / tan(45)x -50 =1 / sqrt(3)
Simplifying, we find:x =50 +1 / sqrt(3) ≈51.577 meters
Substitute this value of x back into the first equation to find the height of the building:tan(30) = h / x
sqrt(3) /3 = h /51.577
h ≈51.577 * sqrt(3) /3 ≈29.792 meters
Therefore, the building is approximately 29.792 meters tall
A ladder is leaning against a wall. The ladder makes an angle of60 degrees with the ground. If the foot of the ladder is2 meters away from the wall, how long is the ladder?
Let's assume that the length of the ladder is represented by L meters. We can set up a right triangle to represent the situation. The vertical side of the triangle represents the height of the wall, the horizontal side represents the distance between the foot of the ladder and the wall, and the hypotenuse represents the length of the ladder
Using the given information, we can use the cosine function to relate the angle and the sides of the triangle:cos(60) =2 / L
Now, we can solve for L: L =2 / cos(60)L =2 /0.5
L =4 meters
Therefore, the length of the ladder is4 meters.
