Solves quadratic in this form...\[ax^2 + bx + c \]
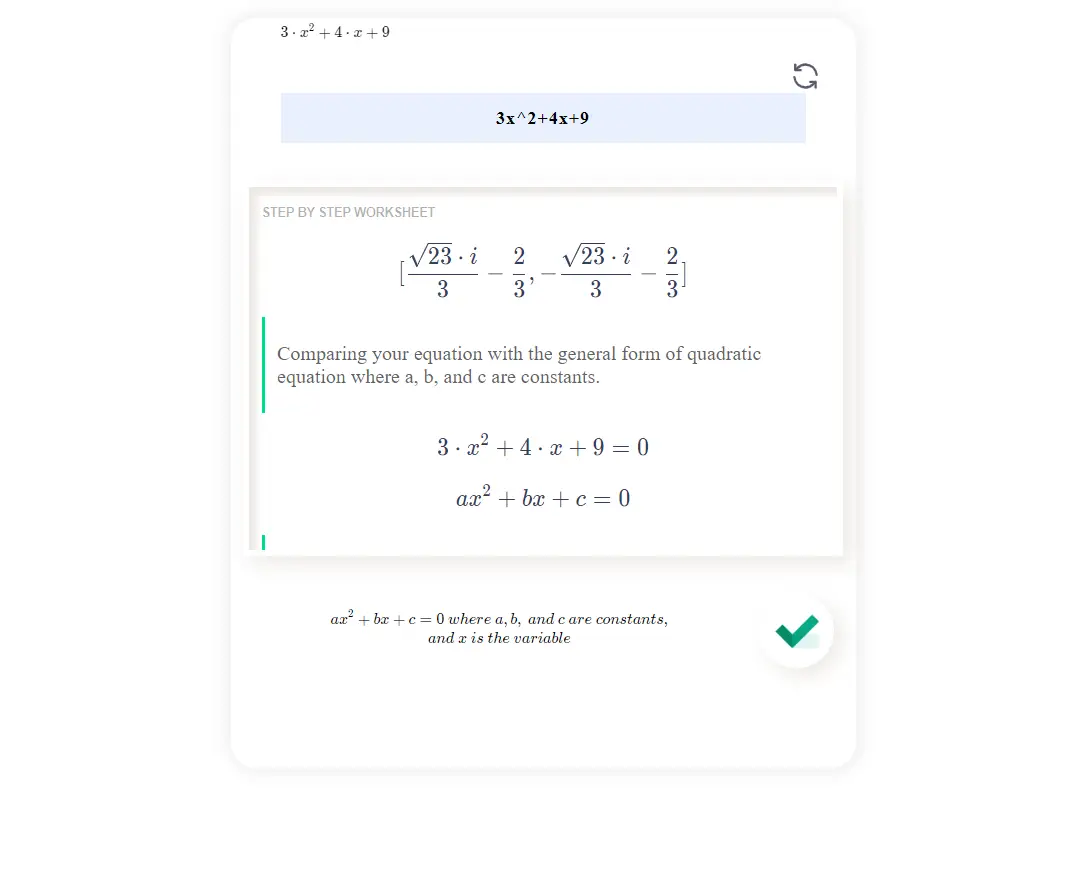
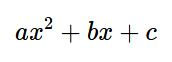
A quadratic equation is a polynomial equation of the second degree, which means it contains a variable raised to the power of 2. The general form of a quadratic equation is: ax^2 + bx + c =0. Where "x" represents the variable, and "a," "b," and "c" are constants, with "a" not equal to zero. The highest power of x in a quadratic equation is 2, and it can have one, two, or no real solutions, depending on the values of a, b, and c.
To begin, let's review what a quadratic equation is. In its general form, a quadratic equation can be written as ax^2 + bx + c = 0, where a, b, and c are constants. The goal is to find the values of x that satisfy this equation.
Using the Quadratic Equation Problem Solver, you can easily determine these values. Here are the steps:
Input the values of a, b, and c into the solver in form of expression.
The solver will identify whether the equation has real solutions, complex solutions, or no solution at all.
If the equation has real solutions, the solver will provide you with the x-values.
It will show you the step-by-step process of solving the equation, which often involves using the quadratic formula: x = (-b ± √(b^2 - 4ac)) / (2a).
The solver will perform the necessary calculations, simplifying the equation along the way.
The Quadratic Equation Problem Solver not only saves you time but also helps you understand the process behind solving quadratic equations. With its clear step-by-step solutions, you can grasp the concepts and improve your overall math skills.
In addition to solving quadratic equations, this solver also covers other areas of math, such as algebra, calculus, statistics, and engineering math. So whether you need help with linear equations, derivatives, probability, or any other math topic, the MathCrave Math AI is here to assist you. Just input your problem, and it will provide you with an accurate solution and detailed explanation.
With the Quadratic Equation Problem Solver and MathCrave Math AI, you can conquer math problems with confidence and ease.
The solutions to a quadratic equation are the values of "x" that make the equation true when substituted into it. These solutions may be real or complex numbers.
The three quadratic functions are:
1. f(x) = ax^2 + bx + c, where a, b, and c are constants.
2. g(x) = a(x - h)^2 + k, where a, h, and k are constants. This is called the vertex form of a quadratic function.
3. h(x) = a(x - r)(x - s), where a, r, and s are constants. This is called the factored form of a quadratic function.
The quadratic formula is a formula used to find the solutions (or roots) of a quadratic equation. A quadratic equation is a second-degree polynomial equation in the form of ax^2 + bx + c = 0, where "a", "b", and "c" are constants. The quadratic formula is given as x = (-b ± √(b^2 - 4ac)) / 2a. It provides the values of "x" where the quadratic equation intersects the x-axis.
To solve a quadratic equation by factorization, follow these steps:
1. Write down the quadratic equation in the form of ax^2 + bx + c = 0, where a, b, and c are coefficients, and x is the variable.
2. Determine the factors of the coefficient 'a' and the constant term 'c' that add up to the coefficient 'b'.
For example, if the equation is 2x^2 + 5x + 3 = 0, the factors of 2 are 1 and 2, and the factors of 3 are 1 and 3. The factors of a quadratic equation should multiply to give 'a' times 'c'.
3. Rewrite the middle term (the bx term) of the equation using the factors determined in the previous step. In this example, the middle term 5x can be rewritten as 2x + 3x.
4. Group the terms and factor by grouping. Group the first two terms and the last two terms together.
In the example, group 2x^2 + 2x and 3x + 3. Factor out the greatest common factor from each group. For the first group, factor out 2x, and for the second group, factor out 3.
Rewriting the equation, we get 2x(x + 1) + 3(x + 1) = 0.
5. Notice that (x + 1) is a common factor in both terms. Factor out (x + 1), and rewrite the equation as (x + 1)(2x + 3) = 0.
6. Set each factor equal to zero and solve for 'x'. In this case, (x + 1) = 0 and (2x + 3) = 0.
7. Solve for 'x' by isolating the variable. For (x + 1) = 0, subtract 1 from both sides to get x = -1. For (2x + 3) = 0, subtract 3 from both sides and divide by 2 to get x = -3/2.
Therefore, the solutions to the quadratic equation 2x^2 + 5x + 3 = 0 are x = -1 and x = -3/2.
There are several methods for solving quadratic equations:
1. Factoring: This method involves factoring the quadratic equation into two binomial factors and setting each factor equal to zero to find the solutions.
2. Completing the square: This method involves rewriting the quadratic equation in a perfect square trinomial form and then solving for the variable.
3. Quadratic formula: This is a formula that provides the solutions to any quadratic equation. It states that for a quadratic equation of the form ax^2 + bx + c = 0, the solutions are given by x = (-b ± √(b^2 - 4ac)) / (2a).
4. Graphing: This method involves graphing the quadratic equation and finding the x-intercepts, which represent the solutions to the equation.
5. Quadratic factoring shortcuts: These are specific techniques for factoring certain types of quadratic equations, such as difference of squares, perfect square trinomials, and sum or difference of cubes.
It is important to note that the method used to solve a quadratic equation may depend on the specific form of the equation or personal preference.
To find the roots of a quadratic equation, you can use the quadratic formula or factorization method.
1. Quadratic Formula:
The quadratic formula is given by:
where a, b, and c are the coefficients of the quadratic equation in the form ax^2 + bx + c = 0.
Calculate the discriminant (b^2 - 4ac) to determine the nature of the roots:
If the discriminant is positive, the equation has two real and distinct roots.
If the discriminant is zero, the equation has two real and equal roots.
If the discriminant is negative, the equation has two complex roots.
Substitute the values of a, b, and c into the quadratic formula and simplify to find the roots.
2. Factorization Method:
If the quadratic equation is factorable, you can find the roots by factoring the equation into two linear factors.
Write down the quadratic equation in the form ax^2 + bx + c = 0.
Try to find two numbers or expressions that multiply to give ac and add up to give b.
Use these numbers or expressions to factorize the quadratic equation into two linear factors.
Set each factor equal to zero and solve for x to find the roots.
The discriminant of a quadratic equation is a mathematical term used to determine the nature of the roots of the equation. It is calculated by taking the square root of the expression b^2 - 4ac, where a, b, and c are the coefficients of the quadratic equation ax^2 + bx + c = 0.
The discriminant can take three different values:
1. If the discriminant is positive (b^2 - 4ac > 0), then the quadratic equation has two distinct real roots. This means that the parabola defined by the equation intersects the x-axis at two different points.
2. If the discriminant is zero (b^2 - 4ac = 0), then the quadratic equation has one real root. In this case, the parabola defined by the equation touches the x-axis at exactly one point.
3. If the discriminant is negative (b^2 - 4ac < 0), then the quadratic equation has no real roots. This means that the parabola defined by the equation does not intersect the x-axis at any point.
The discriminant is important because it helps us understand the nature of the solutions of a quadratic equation. It can be used to determine whether an equation has real or complex roots, and it can also provide information about the geometry and behavior of the corresponding parabola. By analyzing the discriminant, we can gain insights into the graphical representation and solve problems related to the quadratic equation.
No, a quadratic equation can have at most two solutions.
To determine whether a quadratic equation has real or complex solutions, you can use the discriminant. The discriminant is the expression found under the square root sign in the quadratic formula, which is:
Δ = b² - 4ac
where a, b, and c are the coefficients of the quadratic equation in the form: ax² + bx + c = 0.
Based on the value of the discriminant, you can determine the nature of the solutions:
1. If the discriminant (Δ) is greater than 0 (Δ > 0), the quadratic equation has two distinct real solutions.
2. If the discriminant (Δ) is equal to 0 (Δ = 0), the quadratic equation has one real solution (a repeated or double root).
3. If the discriminant (Δ) is less than 0 (Δ < 0), the quadratic equation has complex solutions (non-real solutions).
By evaluating the discriminant, you can determine whether the roots of the quadratic equation are real (distinct or repeated) or complex.
