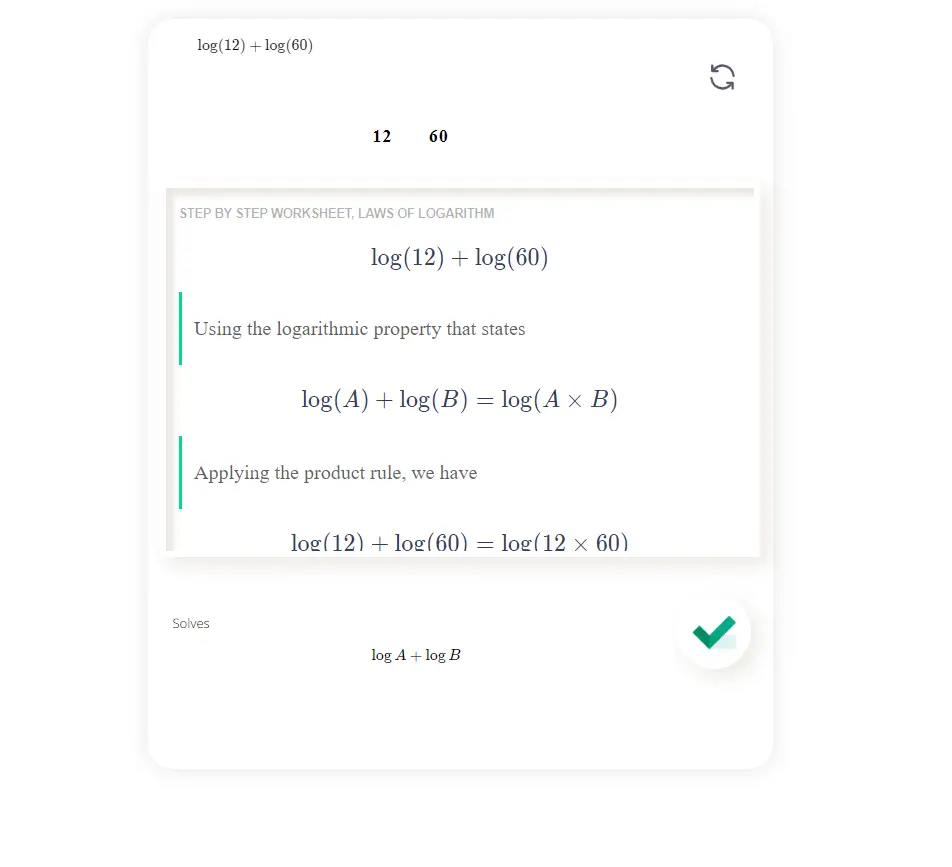
Solves \[\log A + \log B\]
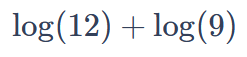
This rule states that the logarithm of a product is equal to the sum of the logarithms of the individual factors.
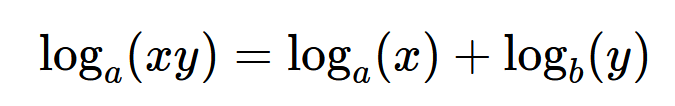
This rule states that the logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator.
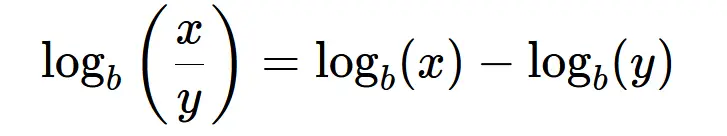
This rule states that the logarithm of a power is equal to the product of the exponent and the logarithm of the base.
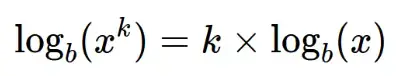
To solve the equation 2^x = 5, take the logarithm (base 2) of both sides to eliminate the exponent.
log_2(2^x) = log_2(5)
Using the logarithmic property that states if log_b(x^y) = y * log_b(x), you can simplify the equation:
x * log_2(2) = log_2(5)
Since log_2(2) = 1, we have:
x = log_2(5)
Using a calculator, we can evaluate log_2(5) to be approximately 2.3219.
Hence, the solution to the equation
2^x = 5 is
x ≈ 2.3219.
To solve the equation 2^x = 8 using base 10, we can take the logarithm (base 10) of both sides to eliminate the exponent.
log_10(2^x) = log_10(8)
Using the logarithmic property that states if log_b(x^y) = y * log_b(x), we can simplify the equation:
x * log_10(2) = log_10(8)
Since log_10(2) is a constant, we can evaluate it to be approximately 0.3010.
x * 0.3010 = log_10(8)
Using a calculator, we can evaluate log_10(8) to be approximately 0.9031.
x * 0.3010 = 0.9031
Simplifying further, we can solve for x:
x ≈ 0.9031 / 0.3010
x ≈ 2.999
Therefore, the solution to the equation 2^x = 8 using base 10 is x ≈ 2.999.
