Complex numbers are numbers that consist of a real part and an imaginary part. They are written in the form a + bi, where a is the real part and bi is the imaginary part, with i representing the square root of -1.
Operations on complex numbers involve addition, subtraction, multiplication, and division. To add or subtract complex numbers, simply add or subtract their real and imaginary parts separately. To multiply complex numbers, distribute and combine like terms. To divide complex numbers, multiply the numerator and denominator by the conjugate of the denominator.
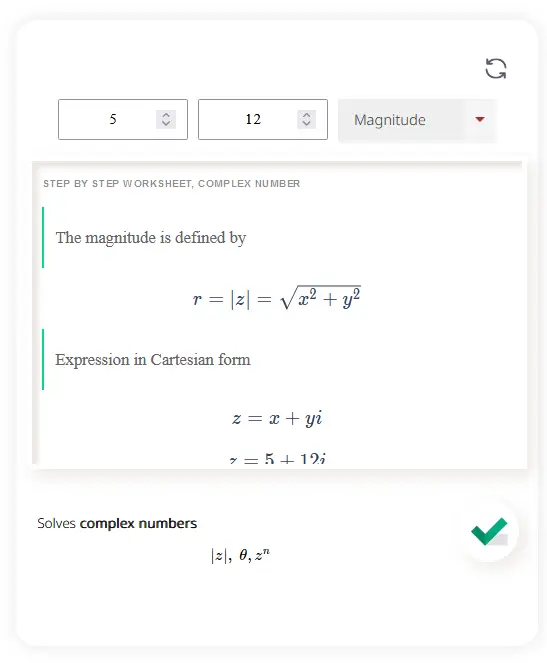
The magnitude of a complex number is the distance from the origin to the point representing the complex number in the complex plane. It is calculated using the formula
|z| = sqrt(a^2 + b^2),
where a is the real part and b is the imaginary part.
The argument of a complex number represents the angle between the positive real axis and the line connecting the origin to the point representing the complex number in the complex plane. It is denoted as arg(z) or theta and can be calculated using the formula
arg(z) = arctan(b/a).
The conjugate of a complex number is obtained by changing the sign of its imaginary part. For a complex number
z = a + bi,
the conjugate is denoted as z* and is equal to a - bi.
The square root of a complex number is a complex number that, when squared, gives the original complex number. To find the square root of a complex number, convert it to polar form, take the square root of the magnitude, and divide the argument by 2.
Proper fractions and improper fractions are two types of fractions based on the relationship between the numerator and the denominator.
A proper fraction is a fraction where the numerator is smaller than the denominator. For example, 1/4, 3/5, and 7/8 are all proper fractions.
An improper fraction is a fraction where the numerator is equal to or greater than the denominator. For example, 5/4, 9/5, and 15/8 are all improper fractions.
It's important to note that both proper fractions and improper fractions can be used to represent parts of a whole or a group. The difference lies in the relationship between the numerator and the denominator.
A mixed number is a combination of a whole number and a proper fraction. It is written in the form of a whole number followed by a space and then a proper fraction. For example, 3 1/2 is a mixed number.
The whole number part represents the whole units, and the fraction part represents a part of a whole. Mixed numbers can also be written as improper fractions by converting the whole number part into fractions.
Explanation: In this fraction, the numerator (2) is smaller than the denominator (5), indicating that we have 2 out of 5 equal parts.
It is a proper fraction because the numerator is less than the denominator, hence the fraction can not be simplified further.
How it works: In this fraction, the numerator (4) is smaller than the denominator (8), indicating that we have 4 out of 8 equal parts and can be reduced to 1/2 when simplified.
It is also a proper fraction because the numerator is less than the denominator.
In this fraction, the numerator (7) is larger than the denominator (4), indicating that we have 7 out of 4 equal parts. It is an improper fraction because the numerator is greater than the denominator.
How to solve this: In this fraction, the numerator (11) is larger than the denominator (6), indicating that we have 11 out of 6 equal parts. It is also an improper fraction because the numerator is greater than the denominator.
Explanation: In this fraction, the numerator (5) is larger than the denominator (2), indicating that we have 5 out of 2 equal parts. It is an improper fraction as the numerator is greater than the denominator.
The Fractions Calculator is an invaluable tool for anyone working with fractions. Whether you're a student trying to simplify fractions or an engineer needing to perform complex calculations, this calculator is here to make your life easier.
Simply input your fraction, and the calculator will provide you with the simplified form, along with step-by-step explanations. With its user-friendly interface and accurate results, the MathCrave Fractions Calculator takes the hassle out of dealing with fractions and ensures you get the correct answers every time. Say goodbye to manual calculations and hello to a faster, more efficient way of working with fractions.
