Solves orthocenter of a triangle in this form \[A(x,y), B(x_2,y_2), C(x_3,y_3)\]
The orthocenter of a triangle is a point of concurrency, which means it is the point where three altitudes of a triangle intersect. An altitude is a line segment drawn from a vertex of a triangle perpendicular to the opposite side, or an extension of that side.
The orthocenter is not always located inside the triangle; it can also be outside or on the triangle depending on the type of triangle.
It is an important point in triangle geometry and has various properties that can be studied and used in problem-solving.
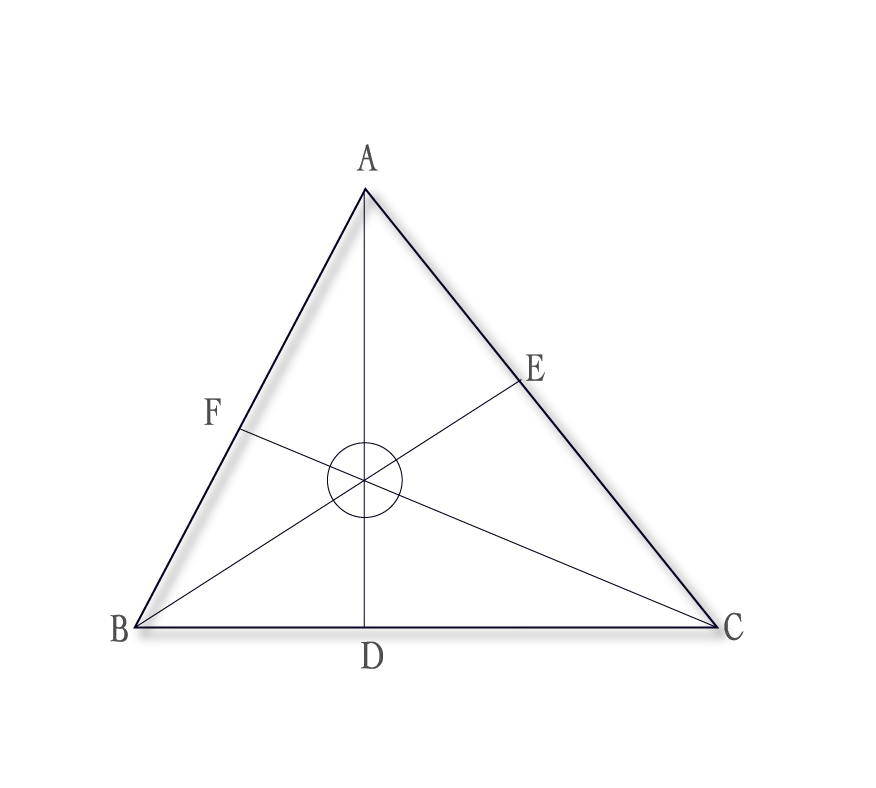
Step 1: Draw the given triangle and label the vertices as A, B, and C.
Step 2: Find the slopes of the three sides of the triangle using the slope formula or by comparing the coordinates of the vertices.
Step 3: Use the slope-intercept form of a line (y = mx + b) to write the equations of the altitudes passing through each vertex. To find the equation of the altitude from vertex A, first find the slope of the line perpendicular to side BC (opposite to vertex A), and then use the point-slope form of a line with the coordinates of vertex A.
Step 4: Solve the system of equations formed by the three equations of the altitudes. This can be done using methods such as substitution or elimination.
Step 5: The solution to the system of equations will give you the coordinates of the orthocenter of the triangle.
Step 6: Verify that the point of intersection obtained in step 5 lies inside the triangle, as the orthocenter should always lie inside the triangle. If the point lies outside the triangle, check your calculations and equations.
