Converts Spherical to Cylindrical \[r=\rho\sin\phi \, \ \theta = \theta , \ z=\rho\cos\phi\]
Spherical coordinates are a coordinate system used to describe the position of a point in three-dimensional space. They are especially useful when dealing with problems involving objects that have a spherical symmetry, such as planets or spheres.
In the spherical coordinate system, a point is described using three values: the radial distance (r), the polar angle (θ), and the azimuthal angle (φ).
Radial Distance (r):
The radial distance is the distance from the origin (usually denoted as O) to the point. It is measured along the straight line connecting the origin to the point.
Polar Angle (θ):
The polar angle is the angle between the positive z-axis and the line connecting the origin to the point. It is measured in the range of 0° to 180° (or 0 to π radians). The polar angle is also known as the inclination angle or the zenith angle.
Azimuthal Angle (φ):
The azimuthal angle is the angle formed between the positive x-axis and the projection of the line connecting the origin to the point onto the xy-plane. It is measured in the range of 0° to 360° (or 0 to 2π radians). The azimuthal angle is also known as the azimuth angle or the azimuthal coordinate.
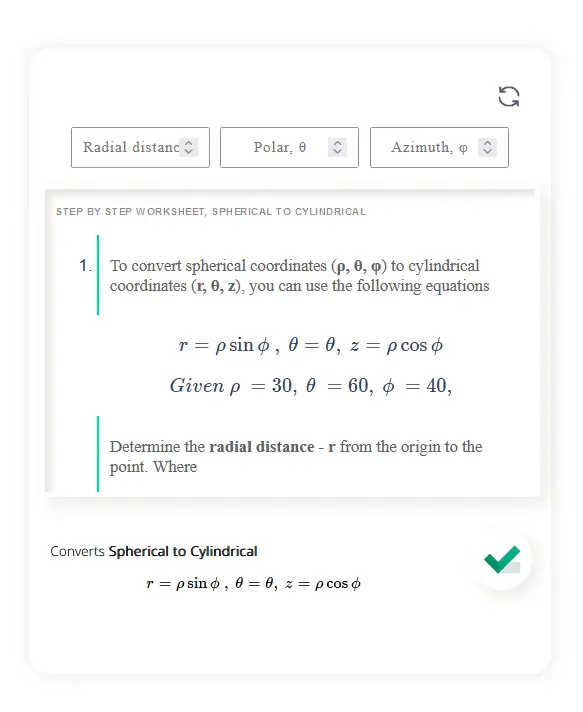
To convert spherical coordinates (ρ, θ, φ) to cylindrical coordinates (r, θ, z), you can use the following equations
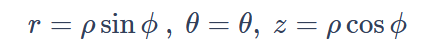
1. Express the radial distance (r) in terms of the cylindrical coordinate ρ:
r = ρ sin(θ)
2. Express the azimuthal angle (φ) in terms of the cylindrical coordinate θ:
φ = θ
3. Determine the value of z using the polar angle (θ), as follows:
z = r cos(θ)
= (ρ sin(θ)) cos(θ)
= ρ sin(θ) cos(θ)
So, the conversion formulas for spherical coordinates to cylindrical coordinates are:
ρ = r sin(φ)
θ = φ
z = r cos(φ)
It's important to note that the ranges of the coordinates vary depending on the specific system used. In the case of cylindrical coordinates, ρ is typically non-negative (ρ ≥ 0), θ is measured in the range of 0 to 2π radians, and z has no restrictions.
