Solves Effective Interest Rate\[r=\left(1+\frac{i}{n}\right)^n-1 \]
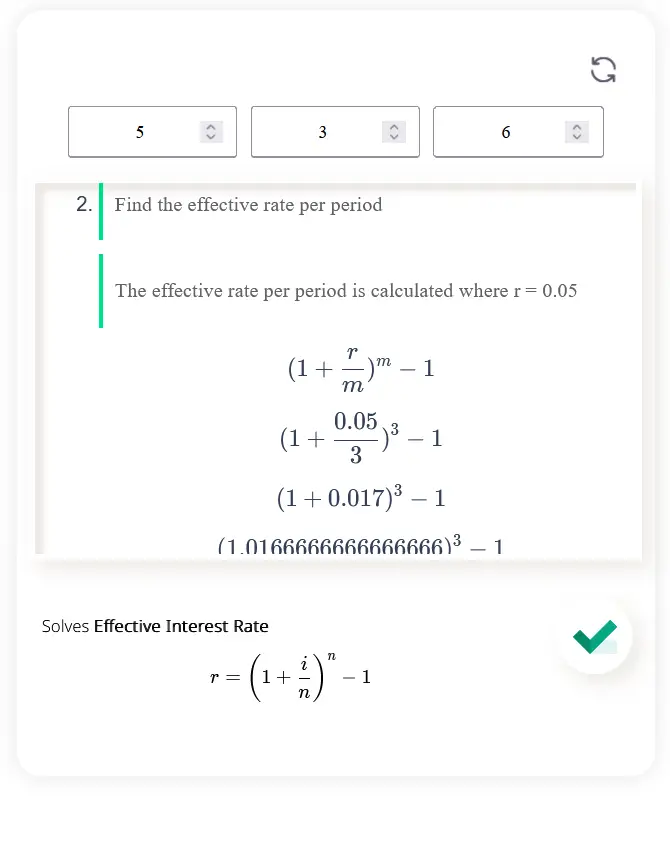
An effective interest rate calculator calculates the true interest rate of a loan or investment, taking into account any additional fees or compounding periods. The effective interest rate is the actual interest rate that will be paid or earned, considering all associated costs.
Components
The rate
The period in month
The number of occurrence
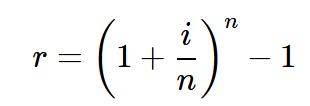
Where i = interest rate charged, r = rate in percentage, and n = is the period it takes
To understand the concept of effective interest rate, let's consider a simple example:
Suppose you want to borrow $10,000 from a bank for one year. The bank charges an annual interest rate of 5%, but they also charge a $100 processing fee upfront. In this case, the effective interest rate would include both the 5% interest and the processing fee.
Using the effective interest rate calculator, you would input the loan amount ($10,000), the annual interest rate (5%), and any additional fees or charges (in this case, $100). The calculator would then determine the true interest rate that accounts for the initial fee.
For Loan Comparison
For example, when comparing two different mortgage loans, each with its own interest rate and associated fees, the effective interest rate can help determine which loan is more cost-effective over the long term.
For Investment
Similarly, in investments such as bonds or certificates of deposit, the effective interest rate helps investors understand the actual return they will earn, considering any fees or compounding effects.
By using an effective interest rate calculator, individuals can make informed financial decisions by evaluating the true cost or return of various loan or investment options. It provides a comprehensive way to assess the financial impact of additional fees and compounding effects over time.
It is worth noting that effective interest rate calculators may vary slightly in their inputs and methods of calculation, but the underlying principle remains the same.
Loan: A loan refers to the act of lending money, property, or other assets to an individual, organization, or entity. It involves the borrowing of a specific amount of money with the agreement to repay the lender over a specified period, generally with interest.
Interest: Interest refers to the amount of money charged for borrowing a loan or the return earned on an investment. It is typically expressed as a percentage of the principal amount. When someone borrows money, they are required to pay back the original amount borrowed (the principal) plus an additional cost, which is the interest.
Rate: In the context of loans and interest, the term "rate" typically refers to the interest rate. It represents the percentage of the loan amount or investment that is charged or earned as interest over a specific period. It is used to determine the cost of borrowing or the return on an investment.
