Solve logarithm in this form \[log_b(x/y) = log_b(x) - log_b(y)\]
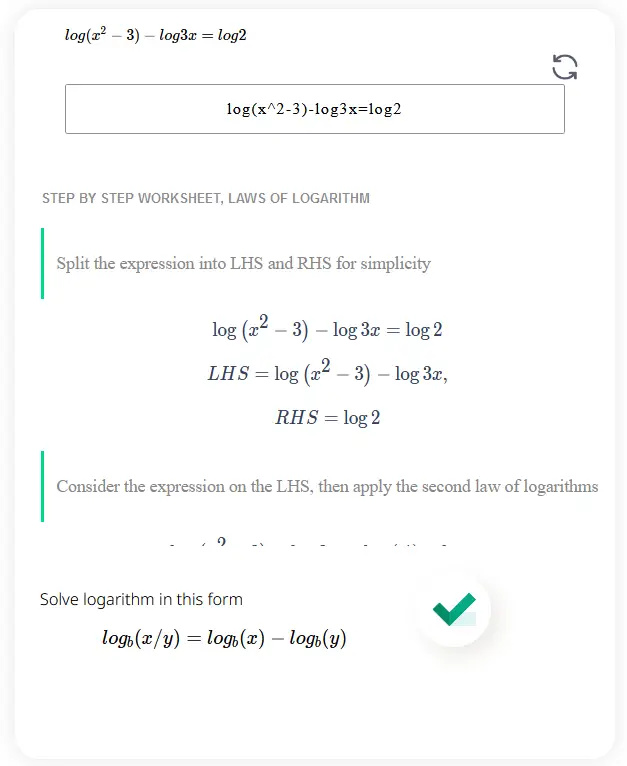
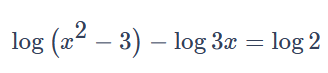
You can solve logarithmic equations using the second law of logarithms, which states that the logarithm of the quotient of two numbers is equal to the difference of their logarithms. To solve equations in this form more efficiently, you can utilize MathCrave log calculator with steps that provides a step-by-step solution.
By entering the expression log(x^2-3) - logx = log 2 into this calculator, it will guide you through the process of solving the logarithmic problem. This step-by-step solution will help you understand the procedure and enable you to solve similar log equations faster in the future. The logarithms calculator with steps simplify any logarithmic complex equation containing the second law of logarithms in the expression.
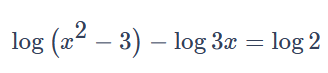
The calculator will first identify the equation's logarithmic form and apply the second law of logarithms. It will simplify the equation by subtracting the logarithms and expressing the quotient as a single logarithm.
Next, the calculator will eliminate the logarithm by converting the equation into an exponential form. It will exponentiate both sides of the equation with the base of the logarithm (usually 10 or e) to cancel out the logarithmic function.
After simplifying the exponential equation, the log calculator will guide you through the process of isolating the variable. This may involve manipulating the equation algebraically, factoring, or applying appropriate arithmetic operations.
By utilizing this logarithm calculator, you can overcome the complexities of solving logarithmic equations and obtain faster results. The detailed solution provided will enhance your understanding of the logarithmic problem, making it easier for you to tackle similar equations in the future.
