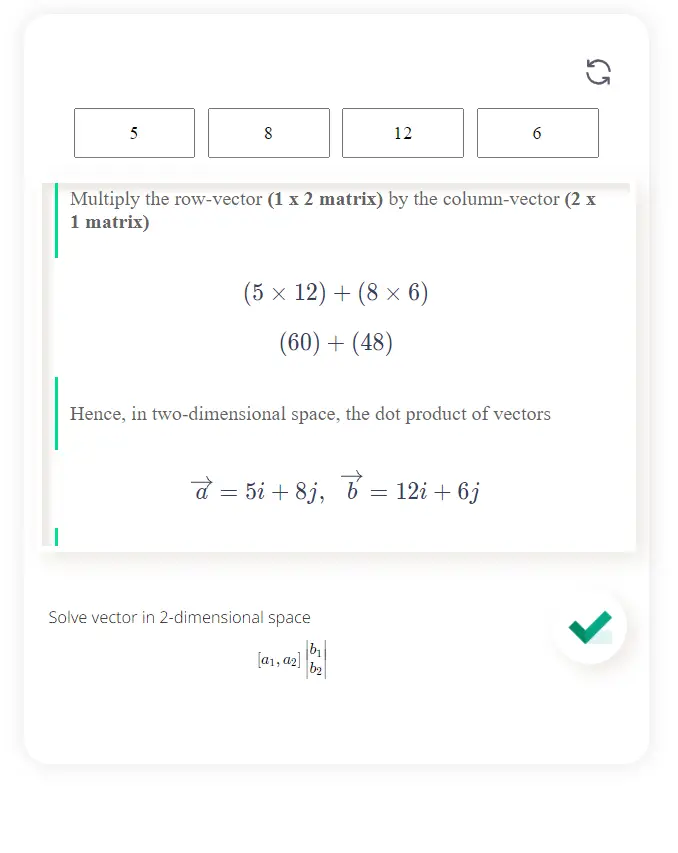
Solve vector in 2-dimensional space\[ [a_1,a_2] \begin{vmatrix} b_1 \\ b_2 \end{vmatrix}\]
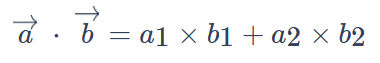
The dot product of two dimensional vectors is a mathematical operation that determines the scalar product of two vectors. It is denoted by a dot (·) between the two vectors.
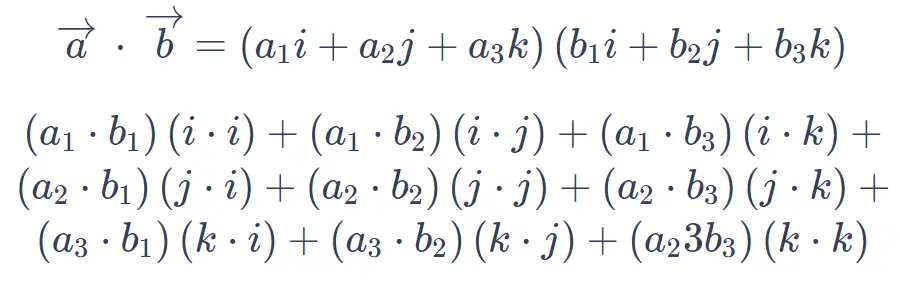
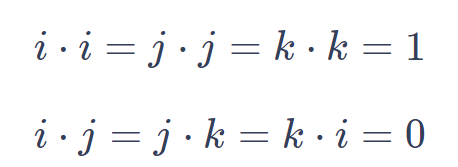
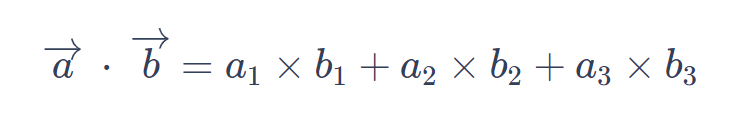
To find the dot product of two dimensional vectors, you can follow these steps:
1. Write down the two vectors in component form. For example, if the vectors are A = (a1, a2) and B = (b1, b2), where a1, a2, b1, and b2 are the components of the vectors.
2. Multiply the corresponding components of the two vectors. In this case, you would multiply a1 with b1 and a2 with b2.
3. Add the products obtained in step 2. This will give you the dot product of the two vectors.
4. The result is a scalar value.
For example, let's find the dot product of A = (2, 3) and B = (4, 1):
A · B = (2 x 4) + (3 x 1) = 8 + 3 = 11
Therefore, the dot product of A and B is 11.
It is important to note that the dot product is commutative, meaning the order of the vectors does not matter. So A · B is equal to B · A.
To solve the dot product of two vectors, follow these steps:
1. Write down the two vectors you want to find the dot product of. For example, let's say we have vector A = [a1, a2, a3] and vector B = [b1, b2, b3].
2. Multiply the corresponding components of the two vectors together. In other words, multiply a1 by b1, a2 by b2, and a3 by b3.
3. Add up the results from step 2. For example, if the results from step 2 are c1, c2, and c3, then the dot product is c1 + c2 + c3.
4. Write down the dot product as a scalar value.
Let A = [2, 3, 4] and B = [1, -2, 5].
Multiply the corresponding components:
a1 x b1 = 2 x 1 = 2
a2 x b2 = 3 x -2 = -6
a3 x b3 = 4 x 5 = 20
Add up the results:
2 + (-6) + 20 = 16
So, the dot product of vectors A and B is 16.
The dot product of two-dimensional vectors is a scalar value obtained by multiplying the corresponding components of the vectors and summing them. It is a simple operation that results in a single value.
On the other hand, the dot product of matrices is a more complex operation. It involves multiplying the corresponding elements of the matrices and summing them up. The resulting matrix is the dot product of the two matrices.
The dot product of two-dimensional vectors is a scalar value, while the dot product of matrices is a matrix.
