Integration answer and graph \[\frac{\left(1+x\right)^2}{\sqrt{x}}\]
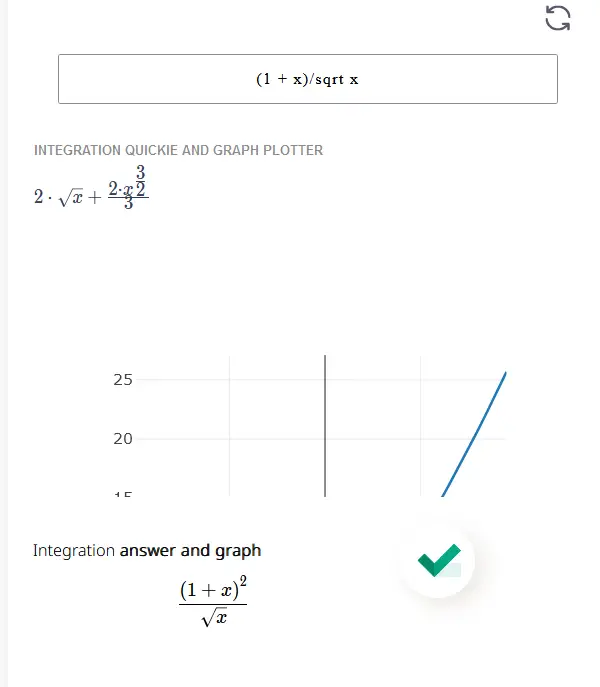
An integration solver is used to integrate a function over a given interval. In the integration process, you have to find the area under a curve, the integral of a function, or the product of two functions. Use this integral solver to evaluate definite integrals, integrate standard functions − cos ax, sin ax, sec 2 ax, cosec 2 ax, cosec ax, cot ax, sec ax, tan ax, eax , 1/x and more.
Enter integral equation or expression (ensure the expressions are correctly formed)
Hit the check mark button to solve calculate and plot your graph
Evaluate the integral ∫(3x^2 +2x +1) dx
Step 1: Distribute the integral sign to each term inside the parentheses:
∫3x^2 dx + ∫2x dx + ∫1 dx
Step 2: Integrate each term separately:
∫3x^2 dx = x^3 + C1 (where C1 is the constant of integration)
∫2x dx = x^2 + C2
∫1 dx = x + C3
Step 3: Combine the results:
∫(3x^2 +2x +1) dx
= x^3 + C1 + x^2 + C2 + x + C3
= x^3 + x^2 + x + C
(where C is the constant of integration)
Evaluate the integral ∫(4x^3 -2x^2 +5) dx
Step 1: Distribute the integral sign to each term inside the parentheses:
∫4x^3 dx - ∫2x^2 dx + ∫5 dx
Step 2: Integrate each term separately:
∫4x^3 dx = x^4 + C1
∫2x^2 dx = (2/3)x^3 + C2
∫5 dx =5x + C3
Step 3: Combine the results:
∫(4x^3 -2x^2 +5) dx
= x^4 + C1 - (2/3)x^3 + C2 +5x + C3
= x^4 - (2/3)x^3 +5x + C
(where C is the constant of integration)
Evaluate the integral ∫(e^x +2x^2) dx
Step 1: Distribute the integral sign to each term inside the parentheses:
∫e^x dx + ∫2x^2 dx
Step 2: Integrate each term separately:
∫e^x dx = e^x + C1
∫2x^2 dx = (2/3)x^3 + C2
Step 3: Combine the results:
∫(e^x +2x^2) dx = e^x + C1 + (2/3)x^3 + C2 = e^x + (2/3)x^3 + C
(where C is the constant of integration)
Evaluate the integral ∫(cos(x) +3sin(x)) dx
Step 1: Distribute the integral sign to each term inside the parentheses:
∫cos(x) dx + ∫3sin(x) dx
Step 2: Integrate each term separately:
∫cos(x) dx = sin(x) + C1
∫3sin(x) dx = -3cos(x) + C2
Step 3: Combine the results:
∫(cos(x) +3sin(x)) dx
= sin(x) + C1 -3cos(x) + C2
= sin(x) -3cos(x) + C
(where C is the constant of integration)
