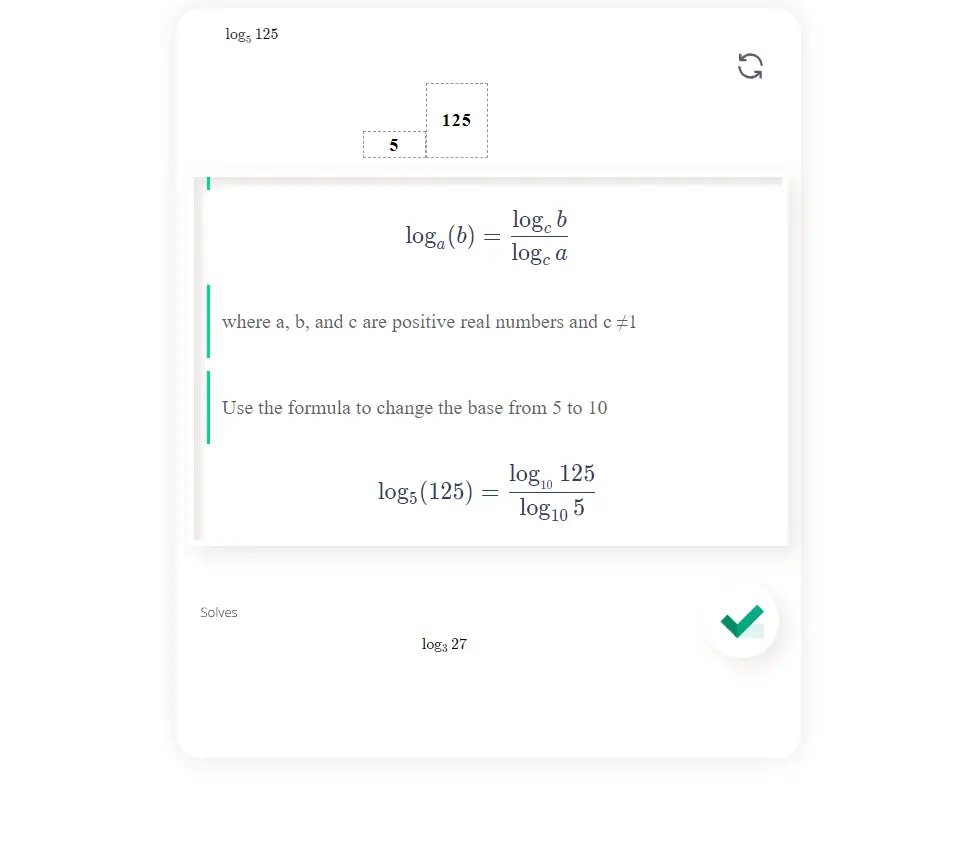
Solves logarithms in this form \[ \log_327\]
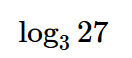
Logarithms change of base is a method used to convert logarithms number with one base to logarithms with another base.
If log_a(x) represents the logarithm of x with base a, and log_b(x) represents the logarithm of x with base b, then the change of base formula is:
log_a(x) = log_b(x) / log_b(a)
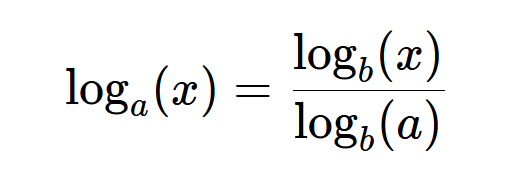
In this formula, log_a(x) represents the logarithm of x with base a, and log_b(x) represents the logarithm of x with base b.
This property allows you to convert logarithms with one base to logarithms with another base. By using this formula, we can evaluate logarithms with different bases using logarithms with bases that are more easily calculated, such as the common logarithm (base 10) or the natural logarithm (base e).
To solve logarithms with a change of base, you can follow these steps:
Identify the given logarithm and the desired base for the new logarithm.
Apply the change of base formula: log_a(x) = log_b(x) / log_b(a), where log_a(x) is the given logarithm, log_b(x) is the new logarithm, and log_b(a) is the logarithm of the desired base.
Calculate the logarithms of the given number and the desired base using the same base (such as the common logarithm or natural logarithm).
Substitute the values into the change of base formula and simplify to find the value of the new logarithm.
Solve log_3(27)
Using the common logarithm (base 10).
Step 1: Identify the given logarithm and the desired base.
Given logarithm: log_3(27)
Desired base: log_10(27)
Step 2: Apply the change of base formula.
log_3(27) = log_10(27) / log_10(3)
Step 3: Calculate the logarithms using the common logarithm.
log_10(27) ≈ 1.4314
log_10(3) ≈ 0.4771
Step 4: Substitute the values into the formula and simplify.
log_3(27) ≈ 1.4314 / 0.4771 ≈ 3
Therefore, log_3(27) is approximately equal to 3.
Solve log_2(16) using the base 10.
Step 1: Identify the given logarithm and the desired base.
Given logarithm: log_2(16)
Desired base: log_10(16)
Step 2: Apply the change of base formula.
log_2(16) = log_10(16) / log_10(2)
Step 3: Calculate the logarithms using the common logarithm.
log_10(16) ≈ 1.2041
log_10(2) ≈ 0.3010
Step 4: Substitute the values into the formula and simplify.
log_2(16) ≈ 1.2041 / 0.3010 ≈ 4
Hence, log_2(16) is approximately equal to 4.
