Solves percentage addition using \[\%addition=a+b\% \times =\frac{a}{100} \]
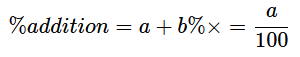
Percentage increase commonly used to quantify and compare changes in various contexts, such as sales figures, population growth, or price fluctuations.
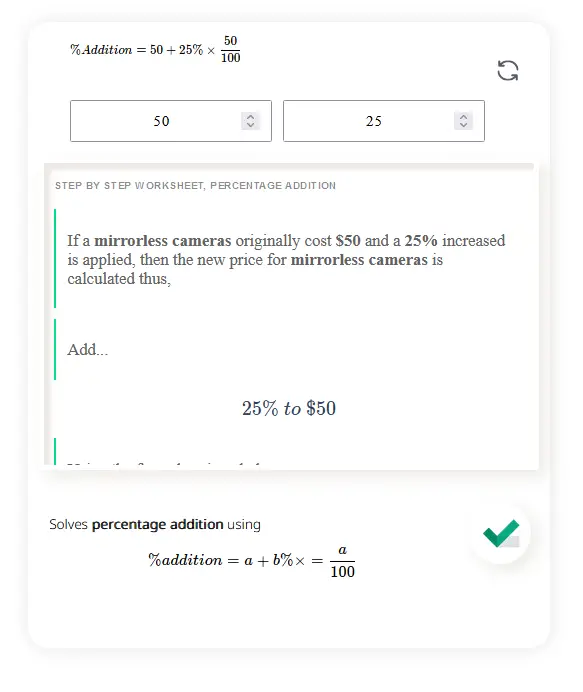
To understand how to use percentage increase or addition in a real-life example, let's consider an individual's salary increment. Suppose John's annual salary was $50,000, and he received a 10% increase. To calculate his new salary, we multiply the original salary by 10% (or 0.10) and add it to the original amount:
Salary increase = $50,000 * 0.10 = $5,000
New salary = $50,000 + $5,000 = $55,000
In this case, John's salary increased by 10% or $5,000, resulting in a new salary of $55,000.
Another example could be a store offering a discount on a product. Let's say a laptop initially costs $1,000, but the store offers a 20% discount. To calculate the discounted price, we multiply the original price by 20% (or 0.20) and subtract it from the original amount:
Discount amount = $1,000 * 0.20 = $200
Discounted price = $1,000 - $200 = $800
In this scenario, the store is offering a 20% discount, resulting in a reduced price of $800.
These examples demonstrate how percentage increase or addition can be used in real-life situations to calculate changes in quantities, such as salary increments or discounts on products. It is a useful tool for analyzing and comparing changes and understanding the impact of percentage variations in various contexts.
It is commonly used to measure growth, inflation, interest rates, and various other economic and mathematical concepts. Understanding how to calculate and apply percentage increases or additions is essential in many real-life scenarios, such as finance, sales, and statistics. Here are three examples that illustrate the practical applications of percentage increase or addition:
Inflation Rate: Suppose the inflation rate in a country is 2%. This indicates that the average price of goods and services has increased by 2% compared to the previous year. For instance, if a loaf of bread cost $2 last year, with a 2% increase, it would now cost $2.04. This calculation helps individuals and businesses adjust their budgets and anticipate changes in prices.
Salary Increase: Let's say an employee receives a 5% salary increase. If their original salary was $50,000, the increase would amount to $2,500 (5% of $50,000). As a result, their new salary would be $52,500. This calculation demonstrates how percentage increase can determine the new value of a salary, allowing individuals to negotiate or evaluate their income changes.
Sales Growth: Consider a retail store that experiences a 10% increase in sales over a year. If their total sales revenue was $1 million, the growth would result in an additional $100,000 in revenue. Consequently, the store's total sales for the year would amount to $1.1 million. This example showcases how businesses use percentage increase to assess their growth and make informed decisions regarding expansion, marketing strategies, and resource allocation.
