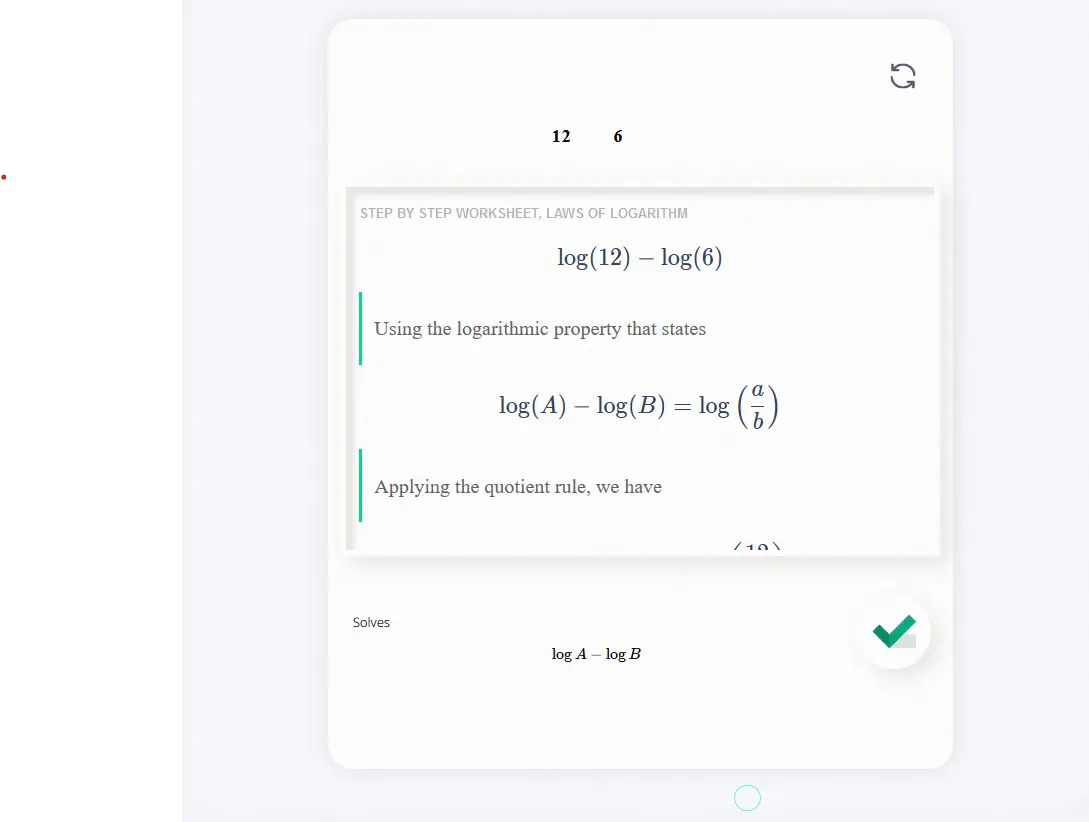
Solves \[\log A - \log B\]
The logarithm rules of quotient are a set of rules that help simplify and solve logarithmic expressions involving division. These rules are derived from the properties of logarithms and can be used to manipulate and solve logarithmic equations.
The quotient rule states that the logarithm of a quotient is equal to the difference of the logarithms of the numerator and denominator. Mathematically, it can be expressed as:
log base b (x / y) = log base b (x) - log base b (y)
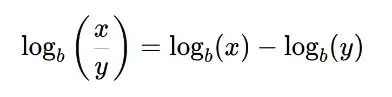
The logarithm rules of quotient state that the logarithm of a quotient of two numbers is equal to the difference of the logarithms of the numbers. Mathematically, this can be written as:
log(base a) (x/y) = log(base a) (x) - log(base a) (y)
Here, "log(base a)" represents the logarithm function with base "a", and "x" and "y" are the numbers in the quotient.
To solve a problem using the logarithm rules of quotient, follow these steps:
1. Identify the numbers in the quotient. Let's say we have x and y.
2. Apply the logarithm with the same base to both x and y.
3. Subtract the logarithms of x and y.
For example, let's say we have to find log(base 3) (5/2). Following the steps, we get:
log(base 3) (5/2) = log(base 3) (5) - log(base 3) (2)
Now, you can evaluate the logarithms of 5 and 2 individually using the base 3 logarithm function.
Example: log(base 2) (8 / 2)
Step 1: Apply the quotient rule.
log(base 2) (8 / 2) = log(base 2) 8 - log(base 2) 2
Step 2: Simplify the logarithms.
log(base 2) 8 = 3 (since 2^3 = 8)
log(base 2) 2 = 1 (since 2^1 = 2)
Step 3: Substitute the simplified logarithms back into the equation.
log(base 2) (8 / 2) = 3 - 1 = 2
Therefore, log(base 2) (8 / 2) = 2.
Solve the logarithmic equation log(base 5) (125 / 25).
Step 1: Apply the quotient rule.
log(base 5) (125 / 25) = log(base 5) 125 - log(base 5) 25
Step 2: Simplify the logarithms.
log(base 5) 125 = 3 (since 5^3 = 125)
log(base 5) 25 = 2 (since 5^2 = 25)
Step 3: Substitute the simplified logarithms back into the equation.
log(base 5) (125 / 25) = 3 - 2 = 1
Therefore, log(base 5) (125 / 25) = 1.
