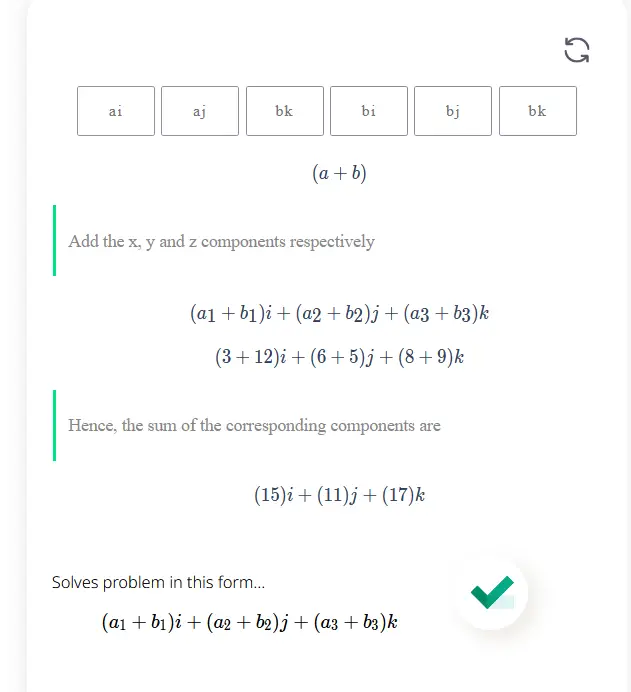
Solves problem in this form... \[(a_1 + b_1)i + (a_2 + b_2)j+ (a_3 + b_3)k \]
A vector addition calculator is a powerful tool that allows users to effortlessly perform arithmetic operations involving vectors. It simplifies the process of adding vectors together by providing an efficient and accurate method for calculating their resultant vector.
Simply input the coordinates or magnitudes and angles of the vectors you wish to add, and the calculator quickly computes the resultant vector.
This tool is particularly useful in various fields, including physics, engineering, and mathematics. It enables professionals and students to perform vector addition calculations in a fraction of the time it would take by manual methods. Moreover, it minimizes the risk of human error, guaranteeing reliable and consistent results.
A vector addition calculator often offers advanced features, such as the ability to compute the dot product or cross product of vectors. These functionalities further enhance its usefulness and versatility, as they allow users to perform more complex vector operations effortlessly.
To solve the vector addition of a(3,5,7) and b(5,6,9), follow these steps:
1. Write down the given vectors: a = (3,5,7) and b = (5,6,9).
2. Add the corresponding components of the vectors. In this case, add the x-components, y-components, and z-components separately:
- For the x-component: 3 +5 =8
- For the y-component: 5 +6 =11
- For the z-component: 7 +9 =16
3. Write the resulting vector by combining the components obtained in the previous step.
The resulting vector is the sum of vectors a and b: (8,11,16).
Therefore, the vector sum of a(3,5,7) and b(5,6,9) is (8,11,16).
