Common geometric shapes can be easily calculated for their area and perimeter with the use of reference formulas on geometric formulas, common shapes.
Geometric formulas provide easy reference formulas that can be used to calculate the area and perimeter of various shapes. These shapes include regular polygons that circumscribe a circle, regular polygons that are inscribed in a circle, triangles that circumscribe or inscribe a circle, as well as parallelograms, rectangles, ellipses, and segments of a parabola.
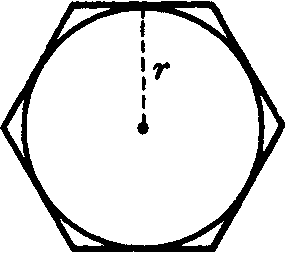
The area of a regular polygon of n sides circumscribing a circle of radius r can be calculated using the formula
A = ½nr2sin(2π/n).
The perimeter of a regular polygon of n sides circumscribing a circle of radius r can be calculated using the formula
P = n r sin (2π/n).
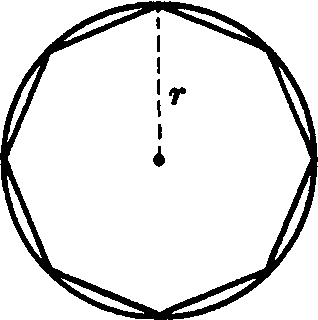
The area of a regular polygon of n sides inscribed in a circle of radius r can be calculated using the formula
A = ½nr2cot(π/n).
The perimeter of a regular polygon of n sides inscribed in a circle of radius r can be calculated using the formula
P = nr.
The radius of a circle circumscribing a triangle of sides a,b,c can be calculated using the formula
r = abc/4S,
where S is the sem-iperimeter of the triangle. The radius of a circle inscribed in a triangle of sides a,b,c can be calculated using the formula
r = (s–a)(s–b)(s–c)/2s,
where s is the semi-perimeter of the triangle.
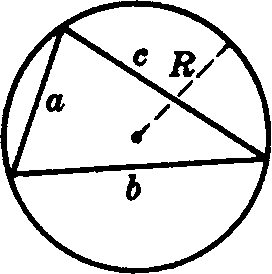
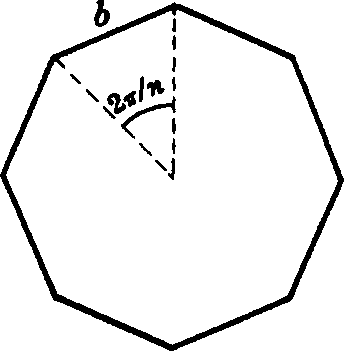
The area of a regular polygon of n sides each of length b can be calculated using the formula
A = ½nb2sin(2π/n).
The perimeter of a regular polygon of n sides each of length b can be calculated using the formula
P = nb
The area of a trapezoid of altitude h and parallel sides a,b can be calculated using the formula
A = ½(a+b)h.
The perimeter of a trapezoid of altitude h and base a, b can be calculated using the formula
P = (a+b+2h).
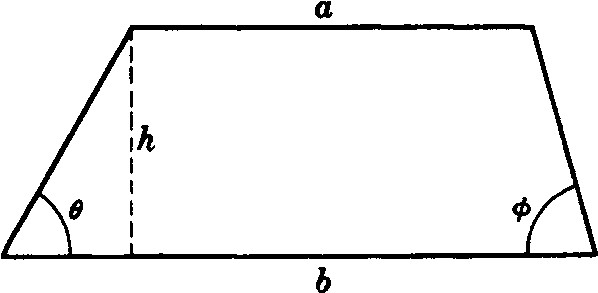
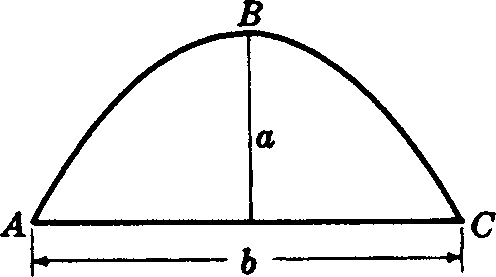
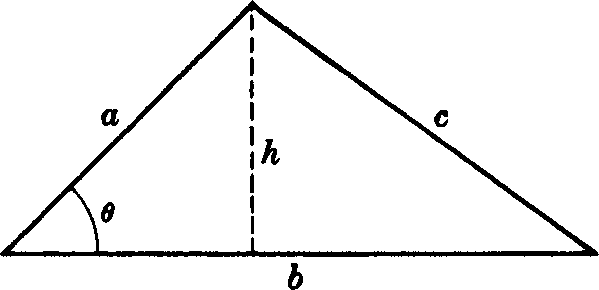
The area of a triangle of altitude h and base b can be calculated using the formula
A = ½bh.
The perimeter of a triangle of altitude h and base b can be calculated using the formula
P = b+2h.
The area of a parallelogram of altitude h and base b can be calculated using the formula
A = bh
The perimeter of a parallelogram of altitude h and base b can be calculated using the formula
P = 2(b+h)

The area of a rectangle of length b and width a can be calculated using the formula
A = ab.
The perimeter of a rectangle of length b and width a can be calculated using the formula
P = 2(a+b).

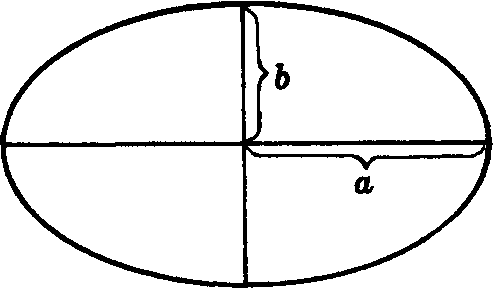
The area of an ellipse of semi-major axis a and semi-minor axis b can be calculated using the formula
A = πab.
The perimeter of an ellipse of semi-major axis a and semi-minor axis b can be calculated using the formula
P = 2π(a+b).
The area of a segment of a parabola can be calculated using the formula
A = ½ab.
The arc length of a segment of a parabola at point ABC can be calculated using the formula
L = 3ab/(2(a+b)).