Solve vector in 3-dimensional space\[ [a_1,a_2,a_3] \begin{vmatrix} b_1 \\ b_2 \\ b_3 \end{vmatrix}\]
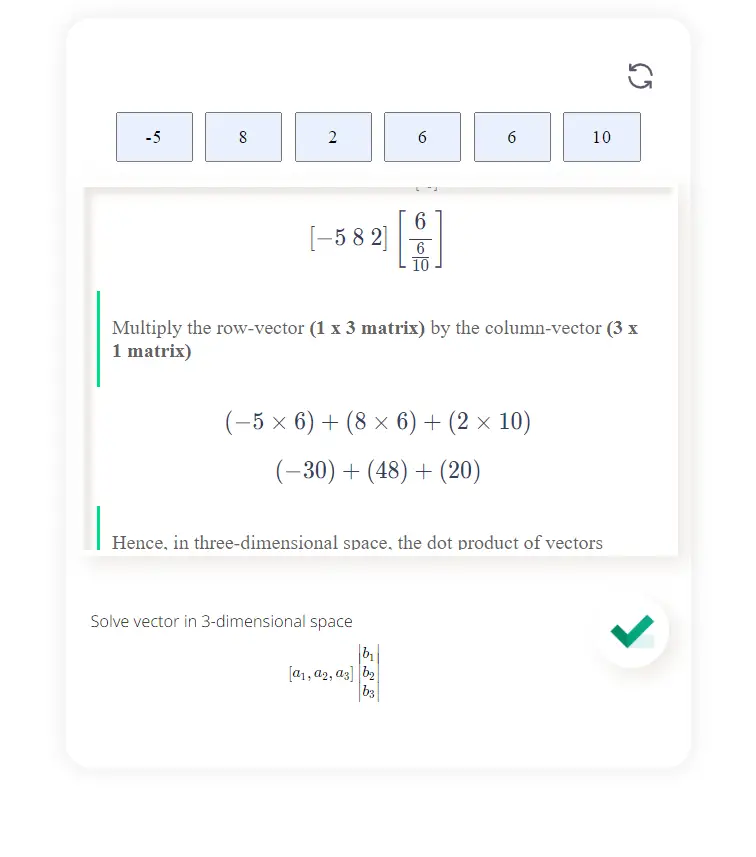
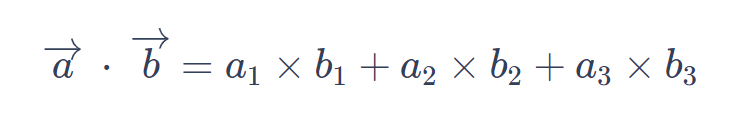
Find the dot product of vector a (2, 3, 4) and b (5. 7, 9) using the calculator
Enter number "2" into the box marked "a1"
Enter number "3" into the box marked "a2"
Enter number "4" into the box marked "a3"
Enter number "5" into the box marked "b1"
Enter number "7" into the box marked "b2"
Enter number "9" into the box marked "b3"
Hit the check mark to solve the dot matrix problem
The dot product, also known as the scalar product, is a mathematical operation performed on two vectors. It results in a scalar value that represents the magnitude of the projection of one vector onto the other vector.
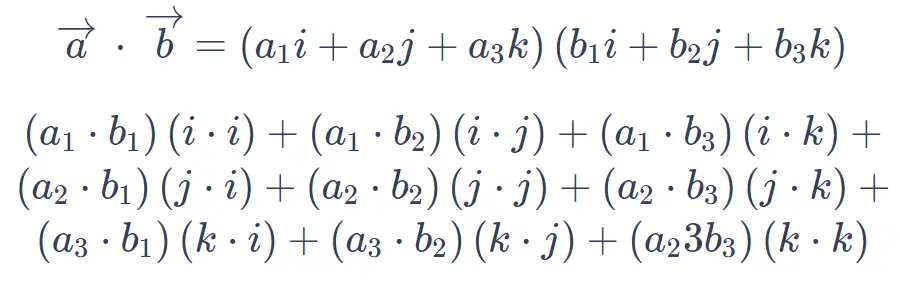
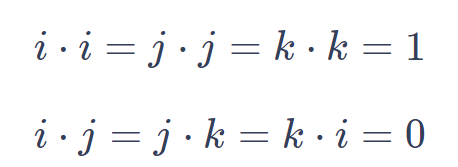
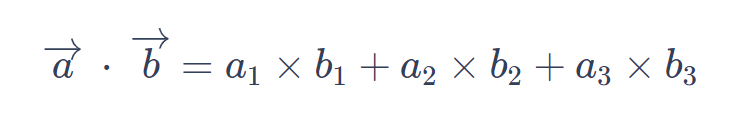
To solve the dot product of two vectors, follow these steps:
1. Write down the two vectors you want to find the dot product of. For example, let's say we have vector A = [a1, a2, a3] and vector B = [b1, b2, b3].
2. Multiply the corresponding components of the two vectors together. In other words, multiply a1 by b1, a2 by b2, and a3 by b3.
3. Add up the results from step 2. For example, if the results from step 2 are c1, c2, and c3, then the dot product is c1 + c2 + c3.
4. Write down the dot product as a scalar value.
Let A = [2, 3, 4] and B = [1, -2, 5].
Multiply the corresponding components:
a1 x b1 = 2 x 1 = 2
a2 x b2 = 3 x -2 = -6
a3 x b3 = 4 x 5 = 20
Add up the results:
2 + (-6) + 20 = 16
So, the dot product of vectors A and B is 16.
To find the dot product of three vectors, you need to perform the dot product operation twice.
Let's say we have three vectors: A = [a1, a2, a3], B = [b1, b2, b3], and C = [c1, c2, c3].
Step 1. First, find the dot product of vectors A and B:
A · B = (a1 * b1) + (a2 * b2) + (a3 * b3).
Step 2. Then, find the dot product of the result from step 1 with vector C:
(A · B) · C = [(a1 * b1) + (a2 * b2) + (a3 * b3)] · C = (a1 * b1 * c1) + (a2 * b2 * c2) + (a3 * b3 * c3).
Let A = [2, 3, 1], B = [4, -1, 5], and C = [-2, 0, 3].
1. Find the dot product of vectors A and B:
A · B = (2 * 4) + (3 * -1) + (1 * 5) = 8 - 3 + 5 = 10.
2. Find the dot product of the result from step 1 with vector C:
(A · B) · C = 10 · C = (10 * -2) + (10 * 0) + (10 * 3) = -20 + 0 + 30 = 10.
Therefore, the dot product of the three vectors A, B, and C is 10.
