Solves logarithms in this form... \[\lg x=2, \log_{10}50 \]
lg x = 2
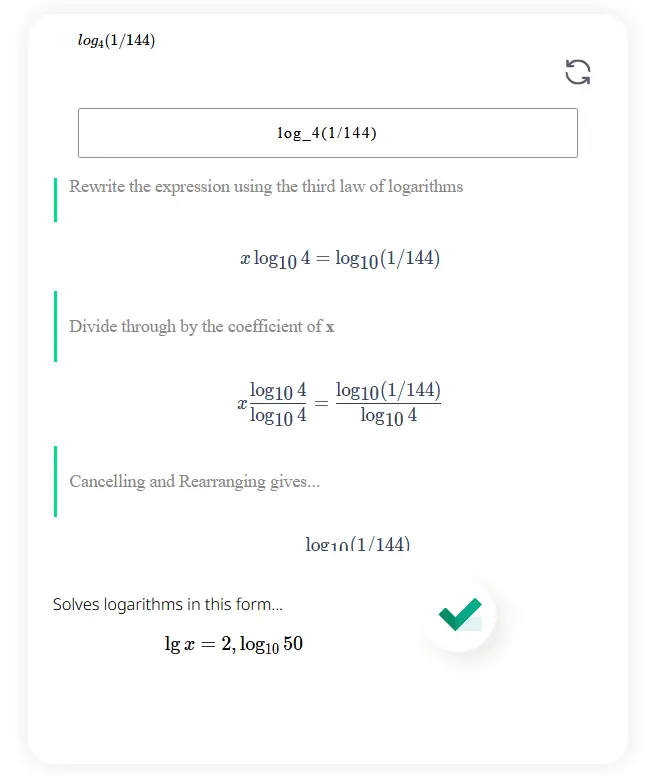
log_4(1/44)
log_{3}27 in this case use bracelet { } to enclose the base not a bracket ( )
log_{5}x=2
2^x=32
The logarithm of a number x, denoted as log(x), is the exponent to which a given base (typically 10 or e) must be raised to obtain that number. In other words, if log(x) = y, then y is the exponent to which the base must be raised to get x.
For example, if log(100) = 2, this means that 10 raised to the power of 2 equals 100. Similarly, if log(e^3) = 3, this means that e (the base of natural logarithms) raised to the power of 3 is e^3.
Logarithms are often used to solve exponential equations, simplify calculations, and convert exponential growth/decay problems into linear form. They have many applications in various fields of mathematics, including algebra, calculus, statistics, and engineering math.
