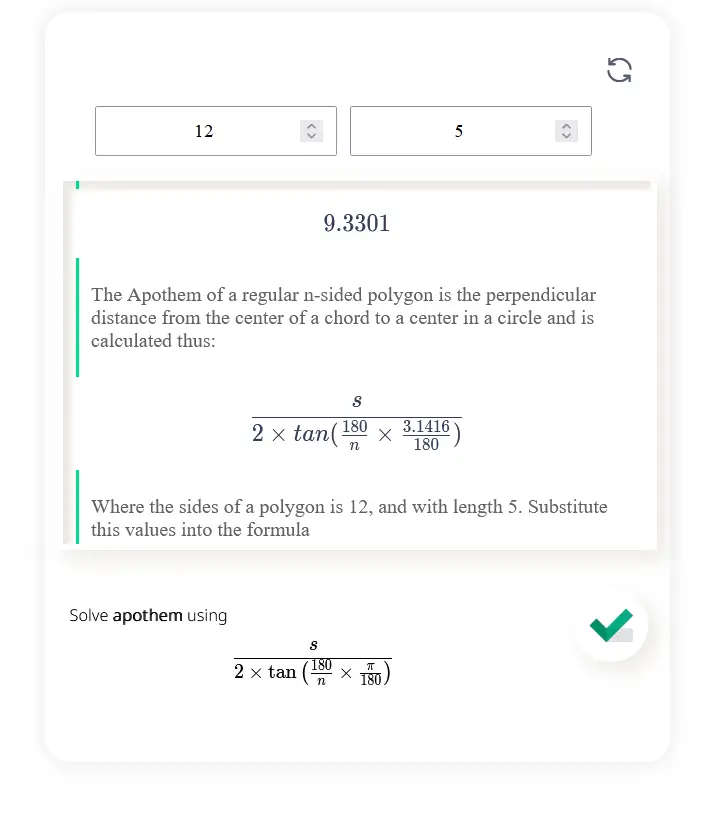
Solve apothem using \[\frac{s}{2\times\tan\left(\frac{180}{n}\times\frac{\pi}{180}\right)} \]
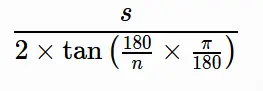
It involves the measuring the distance from the center of a regular polygon to a line that is perpendicular to its side. It is defined as the perpendicular distance from the center to a side of the polygon.
Apothem is the distance from the center to a side of a polygon. Apothem is calculated by dividing the length of the polygon by two times the length of its radius. The apothem can be calculated for any polygon, but it will not be an integer number. The apothem of pentagon solver calculates the apothem of pentagon where number of sides and length are given.
The apothem of a polygon is the distance from the center of the polygon to any of its sides. It is denoted by the letter "a". The formula to calculate the apothem of a regular polygon is:
a = s / (2 * tan(π/n))
where "s" is the length of any side of the polygon and "n" is the number of sides.
The apothem of a polygon, in this case a pentagon, is a line segment drawn from the center of the polygon to one of its sides. It represents the distance from the center to the midpoint of a side. In a regular pentagon, all sides and angles are equal, and so is the apothem. The apothem plays a pivotal role in calculating the area, perimeter, and side length of the pentagon, as well as determining its rotational symmetry.
Example 1:
Let's say we have a regular hexagon with a side length of 8 cm. We want to find the apothem of this hexagon.
Step 1: Identify the given information.
Side length of the hexagon = 8 cm.
Step 2: Apply the formula to calculate the apothem.
a = s / (2 tan(π/n))
a = 8 / (2 tan(π/6))
a = 8 / (2 * tan(π/6))
a ≈ 8 / (2 * 0.5774)
a ≈ 8 / 1.1547
a ≈ 6.9282 cm
Therefore, the apothem of the hexagon is approximately 6.9282 cm.
Step 1: Identify the given information.
- Apothem of the octagon = 5.5 cm.
Step 2: Rearrange the formula to solve for side length.
a = s / (2 tan(π/n))
2 tan(π/n) = s / a
s = a (2 tan(π/n))
Step 3: Substitute the values into the formula and solve for side length.
s = 5.5 (2 tan(π/8))
s = 5.5 (2 * 0.4142)
s = 5.5 * 0.8284
s ≈ 4.5562 cm
Therefore, the length of one side of the octagon is approximately 4.5562 cm.
Step 1: Identify the given information.
Side length of the polygon = 8.
Number of sides of the polygon = 8.
Step 2: Apply the formula to calculate the apothem.
a = s / (2 tan(π/n))
a = 8 / (2 tan(π/8))
a = 8 / (2 tan(π/8))
a ≈ 8 / (2 * 0.4142)
a ≈ 8 / 0.8284
a ≈ 9.6569
The apothem of the polygon is approximately 9.6569 units.
