Solves percentage multiplier using \[\frac{a\times b}{100}=\frac{a}{100}\times\frac{b}{100} \]
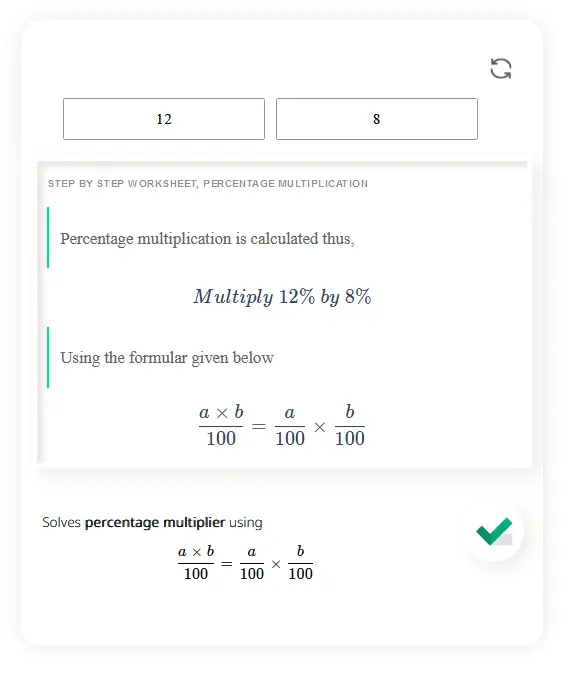
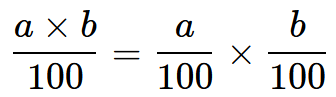
It is a useful tool in various scenarios, such as calculating discounts, markups, or sales tax. To calculate the new value, the percentage is converted into a decimal and then multiplied by the original value.
If the percentage is positive, the value will increase by that percentage, while a negative percentage will result in a decrease. The percentage multiplier provides a quick and efficient way to adjust values and is commonly used in finance, economics, and retail industries.
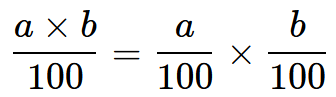
Let's say you want to purchase a product that costs $100, but there is a 20% discount available.
To calculate the discounted price, you would multiply the original price by the discount percentage:
$100 x 20% = $20.
Hence, the discounted price would be $100 - $20 = $80.2.
Suppose you are purchasing an item worth $200, and the sales tax rate is 8%. To find the amount of tax to be paid, you would multiply the purchase amount by the tax rate:
$200 x 8% = $16.
Therefore, the total cost including tax would be $200 + $16 = $216.3.
Consider an investment of $5000 with an annual interest rate of 5%.
To determine the interest earned in one year, you would multiply the initial investment by the interest rate:
$5000 x 5% = $250.
Hence, the interest earned in a year would be $250.4
Suppose a salesperson has made sales worth $10,000, and their commission rate is 4%.
To find the commission earned, you would multiply the sales amount by the commission rate:
$10,000 x 4% = $400.
Therefore, the salesperson's commission would be $400.
