Solve depression using... \[\angle=\frac{h}{s} \]
"Distance" is the horizontal distance between the observer and the object of interest are given. Please note that the result of the arctan function is typically given in radians. However, the calculator provided two different solution in radians and degrees by multiplying the result by (180/π).
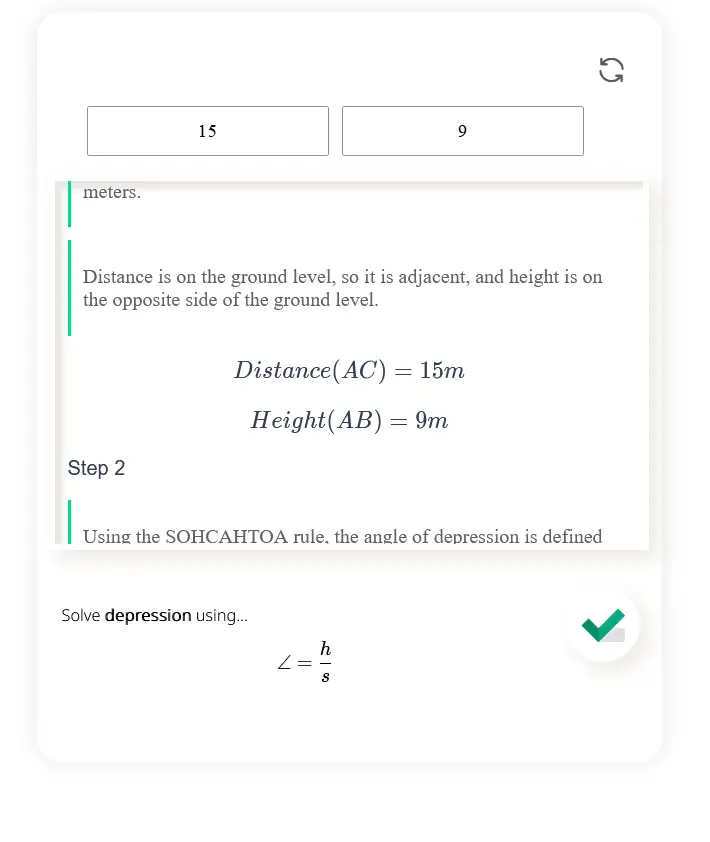
Enter the value for distance and height into the box (numbers only)
Hit the checkmark button to generate your answer.
Example: An electricity pylon stands on horizontal ground. At a point 80 m from the base of the pylon, find the angle of depression of the bottom of the pylon if the height of the pylon is 60 meter long.
The distance will be 80, and height =60, only numbers are used by the calculator to compute the angle of depression using the formula below
The height is the opposite, and the distance is on the adjacent side.
Apply the formula by substituting the value of height and distance for opposite and adjacent sides respectively
The angle of depression is an important concept in trigonometry and geometry. It refers to the angle formed between a line of sight from an observer to a point below them and a horizontal line. This angle is typically measured below the horizontal line.
To better understand the concept, let's explore two worked examples:
Imagine you are standing on top of a tall building and you see a car parked on the street below. You estimate that the car is 100 meters away from the building. If you look straight down to the car, the angle formed between your line of sight and the horizontal line would be the angle of depression.
Let's say you measure this angle to be 30 degrees. This means that the car is located at a 30-degree angle below the horizontal line. By using trigonometric functions such as tangent, you can calculate the height of the building.
Let's say you are standing 10 meters away from a building, and your line of sight to the top of the building forms a 30-degree angle with the ground. To find the height of the building, you can use trigonometry:
Height = distance * tan(angle of depression)
Substituting the given values:
Height = 10 * tan(30°)
Using a scientific calculator or an online trigonometric calculator, you can evaluate the tangent function:
Height = 10 * 0.5774
Height ≈ 5.77 meters
The angle of depression can be calculated using the formula mentioned earlier:
Angle of depression = arctan(height / distance)
arctan(5.77 / 10)
≈ 29.74°
Therefore, the angle of depression to the top of the building is approximately 29.74 degrees.
